You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 삼각 함수 합성 on Google, you do not find the information you need! Here are the best content compiled and compiled by the toplist.Experience-Porthcawl.com team, along with other related topics such as: 삼각 함수 합성 삼각함수 합성 교육과정, 삼각함수 덧셈정리, 삼각함수 합성 문제, 삼각함수 덧셈정리 증명, 삼각함수 합성 주기, 삼각함수 합성 오르비, 삼각함수 합차공식 증명, 삼각함수 합성 최대최소
Table of Contents
삼각함수의 합성 :: winner
- Article author: j1w2k3.tistory.com
- Reviews from users: 642
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about 삼각함수의 합성 :: winner Updating …
- Most searched keywords: Whether you are looking for 삼각함수의 합성 :: winner Updating 01. 삼각함수 합성을 시작하며… 이전에 삼각함수 합성 부분에 대해서 쓴 적이 있는데 글이 너무 오래 되어서 이번 기회에 그떄의 내용을 조금 보완하여 다시 정리를 해 보았습니다. 기본적인 이론과 목적을 바..
- Table of Contents:
삼각함수의 합성
티스토리툴바

삼각함수의 합성 – JW MATHidea
- Article author: jwmath.tistory.com
- Reviews from users: 24616
Ratings
- Top rated: 4.8
- Lowest rated: 1
- Summary of article content: Articles about 삼각함수의 합성 – JW MATHidea Updating …
- Most searched keywords: Whether you are looking for 삼각함수의 합성 – JW MATHidea Updating ■ 삼각함수의 합성 삼각함수의 덧셈정리를 이용하여 ( )를 ( ) 또는 ( ) 꼴의 삼각함수로 나타내어 보자. 1. 사인함수로 합성할 때는 사인함수의 덧셈정리를 사용해야 하므로 곱해지는 삼각함수를 다르게 만..
- Table of Contents:
[5분 고등수학] 삼각함수의 합성
- Article author: hsm-edu-math.tistory.com
- Reviews from users: 22857
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about [5분 고등수학] 삼각함수의 합성 삼각함수 두개를 하나로 합치는 방법이 있습니다. 모든 경우에 다 되는 것은 아니고 각도가 같은 사인과 코사인값을 합치는 것이 가능합니다. …
- Most searched keywords: Whether you are looking for [5분 고등수학] 삼각함수의 합성 삼각함수 두개를 하나로 합치는 방법이 있습니다. 모든 경우에 다 되는 것은 아니고 각도가 같은 사인과 코사인값을 합치는 것이 가능합니다. 삼각함수 두개를 하나로 합치는 방법이 있습니다. 모든 경우에 다 되는 것은 아니고 각도가 같은 사인과 코사인값을 합치는 것이 가능합니다. 아래와 같이 두 가지 방법으로 합칠 수 있..
- Table of Contents:
태그
관련글
댓글2
전체 방문자
최근댓글
태그
티스토리툴바
![[5분 고등수학] 삼각함수의 합성](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FIcRva%2FbtrnjhZpEDm%2FxkWuBhPgrKVmnkXX7cS3H0%2Fimg.png)
삼각함수의 합성의 색다른 관점
- Article author: chemicals1234.tistory.com
- Reviews from users: 28626
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about 삼각함수의 합성의 색다른 관점 Updating …
- Most searched keywords: Whether you are looking for 삼각함수의 합성의 색다른 관점 Updating 현행 교육과정에서 삼각함수의 합 꼴이 나와있을 때, 그것의 최대나 최소를 구하는 방법은 삼각함수의 합성이 있습니다. (물론, 미분해서 극값 찾아도 되지만 굳이…) 삼각함수의 합성이란 무엇이냐… 그러니까..
- Table of Contents:
태그
‘수학📐’ Related Articles
티스토리툴바
삼각함수 합성, 싸인 합성 : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 26241
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about 삼각함수 합성, 싸인 합성 : 네이버 블로그 Updating …
- Most searched keywords: Whether you are looking for 삼각함수 합성, 싸인 합성 : 네이버 블로그 Updating
- Table of Contents:
카테고리 이동
사막별 여행자
이 블로그
생각의나무
카테고리 글
카테고리
이 블로그
생각의나무
카테고리 글

삼각함수 합성 :: 수학공부
- Article author: silverstonec.tistory.com
- Reviews from users: 9535
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about 삼각함수 합성 :: 수학공부 삼각함수의 덧셈정리는 기본으로 외워놓고 시작~. 먼저, 5로 묶어줍니다. 5가 어디서 나왔냐구요..? 여기서요. ① (사인)으로 합성하려면. …
- Most searched keywords: Whether you are looking for 삼각함수 합성 :: 수학공부 삼각함수의 덧셈정리는 기본으로 외워놓고 시작~. 먼저, 5로 묶어줍니다. 5가 어디서 나왔냐구요..? 여기서요. ① (사인)으로 합성하려면. 삼각함수의 덧셈정리는 기본으로 외워놓고 시작~ 먼저, 5로 묶어줍니다. 5가 어디서 나왔냐구요..? 여기서요 ① (사인)으로 합성하려면 공식에 맞게 순서를 바꿔 써주면 이제 눈에 들어오나요..? 말은 빼고..수학공부
- Table of Contents:
삼각함수 합성
티스토리툴바

삼각함수의 합성 – DawoumWiki
- Article author: dawoum.ddns.net
- Reviews from users: 24653
Ratings
- Top rated: 4.1
- Lowest rated: 1
- Summary of article content: Articles about 삼각함수의 합성 – DawoumWiki 물론, 좌변의 식은 유일하게 우변의 식으로 바뀌지는 않는데, 왜햐나면 삼각함수는 근본적으로 주기함수이기 때문입니다. 덧셈정리의 다른 식. …
- Most searched keywords: Whether you are looking for 삼각함수의 합성 – DawoumWiki 물론, 좌변의 식은 유일하게 우변의 식으로 바뀌지는 않는데, 왜햐나면 삼각함수는 근본적으로 주기함수이기 때문입니다. 덧셈정리의 다른 식.
- Table of Contents:
기본 예제
응용예제

See more articles in the same category here: Top 794 tips update new.
삼각함수의 합성
■ 삼각함수의 합성
삼각함수의 덧셈정리를 이용하여 ( )를
( ) 또는 ( )
꼴의 삼각함수로 나타내어 보자.
1. 사인함수로 합성할 때는 사인함수의 덧셈정리를 사용해야 하므로 곱해지는 삼각함수를 다르게 만들면 된다.
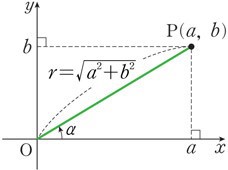
그림과 같이 좌표평면 위의 점 P(a,b)를 잡고, 동경 OP가 x축의 양의 방향과 이루는 각을 라 하면
,
이므로
2. 코사인함수로 합성할 때는 코사인함수의 덧셈정리를 사용해야 하므로 곱해지는 삼각함수를 같게 만들면 된다.
,
이므로
이와 같이 를 ( ) 또는 ( )와 같은 꼴로 나타내는 것을 삼각함수의 합성이라고 한다.
삼각함수의 합성
(1) 사인합성
(2) 코사인합성
( )
사인합성과 코사인합성은 형태는 다르지만 같은 값을 나타낸다.
삼각함수의 합성은 사인함수와 코사인함수의 합으로 표시되어 있는 것을 하나의 삼각함수로 통일할 수 있다. 따라서 삼각함수의 합성을 이용하여 삼각함수의 최대, 최소 또는 함수의 그래프를 그리거나 삼각방정식의 해를 구하는 데 유용하게 사용할 수 있습니다.
예) 를 의 꼴로 나타내보자.
그림과 같이 점 P(1,1)을 잡으면
, 이므로
∴
삼각함수의 합성을 이용하여 삼각함수 의 주기와 최댓값, 최솟값을 구하여 보자.
이므로 주기는 이다.
또한 이므로
따라서 a, b가 동시에 0이 아니면
의 최댓값은 이고, 최솟값은 이다.
예) 의 주기와 최댓값, 최솟값을 구하여 보자.
따라서 최댓값은 2, 최솟값은 –2, 주기는 이다.
삼각함수의 덧셈정리 다양한 증명 삼각함수의 배각 및 반각 공식 (단위원으로 증명) 삼각함수의 주기와 최대, 최소값, 삼각방정식과 부등식 삼각함수의 그래프(sin, cos, tan)와 그 성질 삼각함수 마인드맵 삼각함수로 치환하는 치환적분법(삼각치환법)
반응형
[5분 고등수학] 삼각함수의 합성
반응형
삼각함수 두개를 하나로 합치는 방법이 있습니다. 모든 경우에 다 되는 것은 아니고 각도가 같은 사인과 코사인값을 합치는 것이 가능합니다.
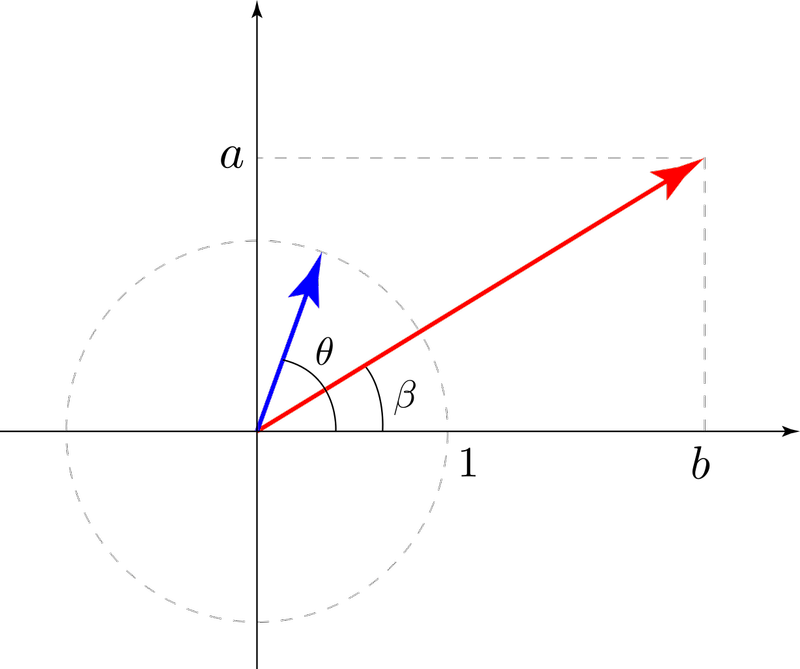
아래와 같이 두 가지 방법으로 합칠 수 있는데요. $\alpha$와 $\beta$의 의미는 뒤에서 설명하겠습니다.
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\sin(\theta+\alpha)$
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\sin(\theta-\beta)$
외워서 풀면 금방 잊습니다. 원리를 이해하고 원리로 푸는 것을 추천드립니다.
하나씩 유도해봅시다.
1) $a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\sin(\theta+\alpha)$
계수인 a와 b를 좌표평면에 표시해보겠습니다. a를 x값으로, b를 y값으로 놓겠습니다.
아래와 같이 직각삼각형을 그려봅시다. 원점에서 생기는 각을 $\alpha$라고 놓겠습니다.
이때 a와 b를 삼각함수로 나타내면 아래와 같습니다.
$a=\sqrt{a^{2}+b^{2}}\cos\alpha$
$b=\sqrt{a^{2}+b^{2}}\sin\alpha$
우리가 유도하려던 식의 좌변은 아래와 같습니다.
$a\sin\theta+b\cos\theta$
위에서 구한 a,b를 대입해줍시다.
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\cos\alpha\sin\theta+\sqrt{a^{2}+b^{2}}\sin\alpha\cos\theta$
아래와 같이 묶어줍시다.
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\left( \cos\alpha\sin\theta+\sin\alpha\cos\theta \right)$
삼각함수의 사인 합공식을 적용합시다.
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\sin(\theta+\alpha)$
2) $a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\sin(\theta-\beta)$
아래 그림과 같이 직각을 제외한 다른 각을 $\beta$로 놓겠습니다.
이때 a와 b를 삼각함수로 나타내면 아래와 같습니다.
$a=\sqrt{a^{2}+b^{2}}\sin\beta$
$b=\sqrt{a^{2}+b^{2}}\cos\beta$
우리가 유도하려던 식의 좌변은 아래와 같습니다.
$a\sin\theta+b\cos\theta$
위에서 구한 a,b를 대입해줍시다.
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\sin\beta\sin\theta+\sqrt{a^{2}+b^{2}}\cos\beta\cos\theta$
아래와 같이 묶어줍시다.
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\left( \sin\beta\sin\theta+\cos\beta\cos\theta \right)$
삼각함수의 코사인 차공식을 적용합시다.
$a\sin\theta+b\cos\theta=\sqrt{a^{2}+b^{2}}\cos(\theta-\beta)$
반응형
삼각함수의 합성의 색다른 관점
현행 교육과정에서 삼각함수의 합 꼴이 나와있을 때, 그것의 최대나 최소를 구하는 방법은 삼각함수의 합성이 있습니다. (물론, 미분해서 극값 찾아도 되지만 굳이…)
삼각함수의 합성이란 무엇이냐… 그러니까 이런 것을 말합니다.
$$a \sin \theta + b \cos \theta = \sqrt{a^2 + b^2} \sin (\theta + \alpha)$$
$$a \sin \theta + b \cos \theta = \sqrt{a^2 + b^2} \cos (\theta – \beta)$$
즉, 같은 각도의 일차 사인함수와 코사인함수의 합을 하나의 삼각함수로 표현할 수 있다는 것이죠. 이렇게 바꾸면 최댓값과 최솟값이 각각 $\sqrt{a^2 + b^2}$ 과 $-\sqrt{a^2 + b^2}$ 이 되는 것을 쉽게 아실 수 있겠습니다. (물론, 합성된 삼각함수의 각의 범위가 $0$부터 $2\pi$같이 평면 상의 같은 거리에 있는 점을 다 표현할 수 있게 되어야겠죠?)
대부분의 문제는 이렇게 최댓값이나 최솟값에 대해 물어봅니다. 하지만, 여기서 많은 학생들이 헷갈려 하는 것이 저 $\alpha$와 $\beta$입니다. 다른 참고서를 보면 $\alpha$와 $\beta$를 $a$와 $b$에 대해서 표현한 식이 참 많이 보이는데, 이를 굳이 힘들게 외우는 학생들이 있습니다. 그러지 않아도 됩니다. 그러면, 여기서 $\alpha$와 $\beta$가 왜 중요한가? 바로 $\theta$가 얼마일 때 최대이고 최소인지 문제에서 묻기 때문이죠.
일반적으로는 $\sin$은 $\dfrac{\pi}{2}$일 때 최대, $\dfrac{3}{2} \pi$일 때 최소이므로
$$ \theta + \alpha = \frac{\pi}{2},\ \frac{3}{2}\pi$$
를 사용하여 $\theta$를 구합니다.
너무 힘들지 않았나요? 그래서, 이를 좀 더 쉽고 색다른 관점에서 바라보고자 합니다.
벡터와 벡터의 내적
(이미 벡터와 내적을 알고 계신 분들은 넘어가셔도 좋습니다)
벡터란, 고등학교 내에서는 크기와 동시에 방향을 가지는 양으로 정의합니다. 그래서 표현도 화살표로 표현하죠. 하지만, 사실 수학에서는 벡터공간이라는 것을 특별히 정의하여 그것의 원소이기만 하면 벡터라고 부릅니다. 그래서 직관적으로 받아들이기 힘든 $n$차원 벡터같은 것도 있죠.
앞으로의 설명을 위해 원점에 대한 위치벡터로 표현하겠습니다. 위치벡터란 어떤 점을 기준점으로 한 벡터로, 만일 좌표계의 원점을 기준점으로 잡았으면, 그 점의 좌표에서 기준점의 좌표를 뺀 것이 위치벡터가 되는 셈이죠.
기준점을 원점으로 잡은경우
즉, 만일 기준점을 원점으로 했다면 그냥 그 점의 좌표가 위치벡터가 된다고 생각하시면 됩니다. 앞으로는 이렇게 원점을 기준점으로 한 위치벡터만을 사용하겠습니다. 이렇게 벡터는 순서쌍으로 표현될 수 있고, 각각 ($x$성분, $y$성분)을 나타냅니다. 앞으로는 위치벡터를 하나의 소문자로 쓰고, 볼드체로 나타내겠습니다.
그리고, 두 벡터 $\mathbf{p} = (p_1 , p_2)$와 $\mathbf{q} = (q_1,q_2)$ 의 내적을 다음과 같이 정의합니다.
$$\mathbf{p} \cdot \mathbf{q} = p_1 q_1 + p_2 q_2$$
이로부터 얻어지는 성질로 벡터의 크기를 $||\mathbf{p}|| = \sqrt{p_1^2 + p_2^2}$ 라고 정의하고, 두 벡터의 사잇각을 $\theta$ 라고 하면, 다음과 같습니다.
$$ \mathbf{p} \cdot \mathbf{q} = ||\mathbf{p}|| \ ||\mathbf{q}|| \cos\theta $$
또한, 내적은 교환법칙이 성립합니다.
그럼, 이를 활용해보죠.
내적을 이용한 삼각함수의 합성
삼각함수의 합성을 보면, $a\sin\theta + b\cos\theta$의 꼴입니다. 뭔가 곱해져 있고, 더해져 있는 꼴이니까 내적과 연관지을 수 있을 것 같습니다. 즉, 이렇게 써보는 것이죠.
$$a\sin\theta + b\cos\theta = (\cos\theta , \sin\theta)\cdot(b,a)$$
굳이 벡터를 $(\sin\theta,\cos\theta)$가 아닌 $(\cos\theta,\sin\theta)$라고 쓴데는 이유가 있습니다. 바로, 좌표평면에서 $(\cos\theta,\sin\theta)$는 반지름의 길이가 $1$인 단위원 위의 한 점을 나타내기 때문이죠. 즉, 좌표평면에 두 벡터 $(\cos\theta,\sin\theta)$와 $(b,a)$를 표현하면 다음과 같습니다.
단위원과 벡터
그렇다면, 내적의 성질에 의해 두 벡터가 평행할 때, 즉 $\theta = \beta$일 때 $\cos(\theta-\beta)$의 값이 $1$이 되므로 최대가 되겠군요. 반대로, 두 벡터의 방향이 반대일 때, 즉 $\theta = \beta + \pi$일 때 $\cos(\theta – \beta)$의 값이 $-1$이 되니 최소가 됩니다.
(위 그림에서 사잇각이 $\theta – \beta$라는 점을 생각하면 됩니다)
다시 말해서, 그냥 최대일 때의 $\theta$는 $\beta$, 최소일 때는 $\beta + \pi$가 된다는 것입니다. 즉, 굳이 어렵게 외우려고 하지 않아도 위 그림만 그리면 된다는 의미이죠.
$(\cos\theta,\sin\theta)$의 크기는 $\sqrt{\cos^ \theta + \sin^2 \theta} = 1$이고 $(b,a)$의 크기는 $\sqrt{a^2 + b^2}$이므로 합성은 다음과 같습니다.
$$a\sin\theta + b\cos\theta = (\cos\theta , \sin\theta)\cdot(b,a) = \sqrt{a^2 + b^2} \cos(\theta-\beta)$$
(우와! 알고 있던 식과 같네요!) 실제로 이 $\beta$가 앞에서의 $\beta$가 맞습니다.
사인에 대해 정리하고 싶으시다면 적절히 $\dfrac{\pi}{2}$를 더하고 빼면 되겠죠.
복소수를 이용한 삼각함수의 합성
(문제를 빨리 풀기만을 위한 사람들은 이 파트를 뛰어넘어도 됩니다.)
삼각함수와 관련있는 것이 또 있습니다. 바로, 복소수인데요. 가로축을 실수축으로, 세로축을 허수축으로 한 복소평면위에 모든 복소수를 대응시킬 수 있습니다. 따라서, 복소수 또한 벡터처럼 크기와 방향을 가지는 값으로 생각할 수 있습니다. 그리고, 오일러 공식이라는 위대한 공식이 있죠. 다음과 같습니다.
$$e^{i \theta} = \cos\theta + i\sin\theta$$
즉, 모든 복소수를 위와 같은 지수함수꼴로 표현할 수 있다는 것이죠. 일반적으로 복소수 $z$를 다음과 같이 표현할 수 있습니다.
$$z = r e^{i\phi}$$
여기서 $r$은 $z$의 크기, $\theta$는 $z$의 편각입니다.
이를 통해 다시 삼각함수의 합성을 생각해봅시다. 다음과 같은 두 복소수를 생각할 수 있습니다.
$$z_1 = \cos\theta + i\sin\theta$$
$$z_2 = b+ai$$
그러면 각각은 오일러 공식에 의해 다음과 같이 표현될 수 있습니다.
$$z_1 = e^{i\theta}$$
$$z_2 = \sqrt{a^2 + b^2} e^{i\beta}$$
둘을 나눠보죠. 그러면 다음과 같습니다.
$$ \frac{z_1}{z_2} = \frac{\cos\theta+i\sin\theta}{b+ai} = \frac{1}{\sqrt{a^2 + b^2}} e^{i(\theta-\beta)} $$
분모의 실수화를 통해 식을 정리하면,
$$ \frac{(\cos\theta+i\sin\theta)(b-ai)}{\sqrt{a^2 + b^2}} = \frac{(a\sin\theta + b\cos\theta)+(b\sin\theta – a\cos\theta)i}{\sqrt{a^2+b^2}} = e^{i(\theta-\beta)} $$
오일러 공식에 따라 $e^{i(\theta-\beta)} = \cos(\theta-\beta) + i\sin(\theta-\beta)$이므로, 복소수 상등을 적용하면 이렇게 정리될 수 있습니다.
$$ a\sin\theta + b\cos\theta = \sqrt{a^2 + b^2} \cos(\theta-\beta) $$
$$ b\sin\theta – a\cos\theta = \sqrt{a^2 + b^2} \sin(\theta-\beta) $$
오! 이렇게 해도 결과가 나오는군요!
만일 $\sin$에 대해 정리하고 싶으시다면 $\theta$ 대신 $\theta + \dfrac{\pi}{2}$를 대입하면 됩니다.
$$ b\sin\left(\theta+\frac{\pi}{2}\right) – a\cos\left(\theta+\frac{\pi}{2}\right) = a\sin\theta + b\cos\theta = \sqrt{a^2 + b^2} \sin\left(\theta + \left(\frac{\pi}{2}-\beta\right)\right) = \sqrt{a^2 + b^2} \sin(\theta+\alpha) $$
단, 여기서 $\alpha = \dfrac{\pi}{2} – \beta$입니다. 이도 앞에서의 $\alpha$가 맞습니다.
마치며
이 방법이 익히는데 조금 걸릴지는 몰라도 유용하게 사용하면 정말 좋은 방법입니다. 뭔가 위상자와도 관계가 있는것 같습니다. 그것은 한번 개인적으로 생각하면 좋을 것 같습니다.
So you have finished reading the 삼각 함수 합성 topic article, if you find this article useful, please share it. Thank you very much. See more: 삼각함수 합성 교육과정, 삼각함수 덧셈정리, 삼각함수 합성 문제, 삼각함수 덧셈정리 증명, 삼각함수 합성 주기, 삼각함수 합성 오르비, 삼각함수 합차공식 증명, 삼각함수 합성 최대최소

