Top 45 유니티 Quaternion 연산 The 195 Detailed Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 유니티 quaternion 연산 on Google, you do not find the information you need! Here are the best content compiled and compiled by the toplist.Experience-Porthcawl.com team, along with other related topics such as: 유니티 quaternion 연산 유니티 각도만큼 회전, Quaternion, 유니티 Quaternion, Quaternion Euler, Quaternion angle, Quaternion rotation, 유니티 회전 범위, 유니티 eulerAngles

쿼터니언과 3차원 회전 | Quaternion | 사원수

[유니티 기초] – Quaternion : 네이버 블로그

Article author: blog.naver.com
Reviews from users: 15595 Ratings
Top rated: 4.1
Lowest rated: 1
Summary of article content: Articles about [유니티 기초] – Quaternion : 네이버 블로그 유니티는 오일러 각을 이용해 회전을 직관적으로 조작할 수 있도록 … Quaternion 연산에서 곱셈의 의미: Quaternion A, B 가 있을 때 (A * B) 는 … …
Most searched keywords: Whether you are looking for [유니티 기초] – Quaternion : 네이버 블로그 유니티는 오일러 각을 이용해 회전을 직관적으로 조작할 수 있도록 … Quaternion 연산에서 곱셈의 의미: Quaternion A, B 가 있을 때 (A * B) 는 …
Table of Contents:

블로그

악성코드가 포함되어 있는 파일입니다

작성자 이외의 방문자에게는 이용이 제한되었습니다

[유니티 기초] - Quaternion : 네이버 블로그 — [유니티 기초] – Quaternion : 네이버 블로그

Article author: rito15.github.io
Reviews from users: 29597 Ratings
Top rated: 4.8
Lowest rated: 1
Summary of article content: Articles about 유니티 – Quaternion | Rito15
이렇게 유니티 구현 코드를 열어봐도. 회전 순서는 언제나 ZXY 라고 나온다. 근데 쿼터니언 곱셈 연산을 통해 실제로 테스트 해보면 … …
Most searched keywords: Whether you are looking for 유니티 – Quaternion | Rito15
이렇게 유니티 구현 코드를 열어봐도. 회전 순서는 언제나 ZXY 라고 나온다. 근데 쿼터니언 곱셈 연산을 통해 실제로 테스트 해보면 … Note
Table of Contents:

회전에 대한 정의

[1] 오일러 회전

[2] 로드리게스(축-각) 회전

[3] 벡터 회전 변위

[4] Z Y 표준 기저 변환

eulerAngles

Inverse(rotation)

Angle(a b)

Dot(a b)

Lerp(a b t)

Slerp(a b t)

[1] q1 ⋅ q2

[2] q ⋅ v

[3] q = q1 ⋅ q

Transformrotation

TransformlocalRotation

[1] 트랜스폼 로컬 회전

[2] 트랜스폼 월드 회전

[3] 대상 바라보기

유니티 – Quaternion | Rito15

Article author: hub1234.tistory.com
Reviews from users: 6539 Ratings
Top rated: 3.2
Lowest rated: 1
Summary of article content: Articles about [유니티] Euler, Quaternion 오일러각 쿼터니언 총 정리 쿼터니언은 각 축을 한꺼번에 계산하기 때문에 짐벌락 문제가 발생하지 않는다. Euler angle 과는 다르게 쿼터니언은 4개의 성분(x, y, z, w)으로 … …
Most searched keywords: Whether you are looking for [유니티] Euler, Quaternion 오일러각 쿼터니언 총 정리 쿼터니언은 각 축을 한꺼번에 계산하기 때문에 짐벌락 문제가 발생하지 않는다. Euler angle 과는 다르게 쿼터니언은 4개의 성분(x, y, z, w)으로 … [Unity] Euler, Quaternion 오일러각(짐벌락) 쿼터니언에 대하여! Unity의 Euler 각도는 x,y,z 3개 축을 기준으로 회전시키는 우리가 흔히 알고있는 각도계를 의미한다. 이 각도계를 사용하면 우리 모두 삽질할..
Table of Contents:

[Unity] Euler Quaternion 오일러각(짐벌락) 쿼터니언에 대하여!

태그

공지사항

최근글

[유니티 기초] – Quaternion

Unity [유니티 기초] – Quaternion HHot ・ URL 복사 본문 기타 기능 공유하기 신고하기 유니티는 오일러 각을 이용해 회전을 직관적으로 조작할 수 있도록 인스펙터 뷰에 표시하고 있다. 하지만 내부적으로는 쿼터니언 방식으로 변환하여 회전을 계산한다. 따라서 사용자가 예외적으로 오일러 각 계산을 이용하도록 설정하지 않는 이상 유니티에서 짐벌 락Gimbal Lock 현상은 발생하지 않는다 [오일러 각 Euler Angles] 수학자 오일러가 고안한 개념으로 3차원 공간의 절대 좌표를 기준으로 물체의 회전을 측정하는 방식 1. 장점 – X, Y, Z 세 개의 축을 기준으로 회전하기에 직관적이며 조작하기 쉽다 – 180도가 넘는 회전도 표현할 수 있다 2. 한계 – 오일러 각을 계산하는데 드는 비용이 크다 – 짐벌 락Gimbal Lock: 오일러 각을 이용한 회전은 먼저 회전한 축이 아직 회전하지 않은 축을 함께 회전시킨다. 따라서 두 번째로 회전한 축의 회전 결과로 인해 세 번째 축과 첫 번째 축이 겹쳐질 수 있는데, 이 상태를 짐벌 락이라고 말하며 degree of freedom 을 상실하게 된다(=첫 번째, 세 번째 축 회전이 하나의 축을 기준으로 일어나기에 자유도 손실) [쿼터니언 Quaternion] – 쿼터니언은 4개의 수(x, y, z, w)로 이루어지며 각 성분은 축이나 각도를 의미하는 게 아니라, 하나의 벡터(x, y, z)와 하나의 스칼라(w, roll을 표현)를 의미한다 – 일반적으로 각 성분에 직접 접근 및 수정하지는 않는다. 쿼터니언 수학을 완전히 이해하지 않은 채로 직접 수정하게 되면 의도한 방식으로 작동시키기 어렵기 때문이다 – 오일러 각이 회전순서에 기반하는 반면에 쿼터니언은 세 축을 동시에 회전시키기에 짐벌 락 현상이 발생하지 않는다(x, y, z 성분은 항상 동시에 변화한다) – 벡터가 위치position 임과 동시에 방향direction 이듯이, 쿼터니언은 방향orientation 임과 동시에 회전rotation 이다 – 벡터가 원점과 특정 위치 비교함으로써 방향을 측정하듯이, 마찬가지로 쿼터니언은 회전의 원점과 특정 방향을 비교함으로써 회전을 측정할 수 있다 – 인스펙터 뷰를 Debug모드로 하면 쿼터니언 성분을 볼 수 있다 *directiron: 두 점을 이용해 나타낼 수 있는 방향. ‘~로 향하는 움직임’ *orientation: 세 가지 오일러 각 또는 쿼터니언을 이용해 나타낼 수 있는 방향. ‘~를 향하고 있는 상태’ 1. 장점 – 짐벌락 문제가 없다 – 계산하는데 드는 비용이 적다 2. 한계 – 쿼터니언을 이용한 회전은 하나의 방향orientation에서 다른 방향orientation으로 측정되기에 180도 보다 큰 회전을 표현할 수 없다 – 직관적으로 이해하기 힘들다 짐벌 락 – 3개의 짐벌을 이용해 회전하는 3차원에서 두 개의 짐벌이 겹쳐질 경우 회전축 하나가 사라지는 현상. 겹쳐진 두 개의 축을 더 이상 움직일 수 없게 된다는 의미가 아니라 그 두 개가 하나의 축으로 합쳐져서 각각 회전시켜도 같은 축을 기준으로 회전하게 된다는 의미이다 – 물체가 회전하면 물체의 좌표계가 함께 회전하고 만약 회전하기 전의 좌표축과 회전한 후의 좌표축이 일치하면 데이터가 소실된다 – 오일러 각은 X, Y, Z축으로의 회전값이 같더라도 어떤 순서로 적용되는지에 따라 결과가 달라진다. 즉, 회전순서를 하이러키로 볼 수 있고 따라서 첫 번째로 회전하는 축이 하위 축들을 함께 회전시키게 된다. 마찬가지로 두 번째로 회전하는 축은 세 번째 축을 함께 움직이며 마지막으로 회전하는 축은 혼자만 회전한다. 이렇듯 회전결과가 축의 회전 순서에 의존하는 방식은 짐벌락 문제를 발생시킨다. 다시 말해 회전 축 3개 중 2개가 하나의 평면상에 있게 되는 것이다(회전 축 정보의 손실) – 앞서 설명했듯이 오일러 체계에서의 회전은 회전순서에 기반하므로 어떤 축이 우선하는지 컴퓨터에게 알려줘야 한다. 애니메이션에서의 쿼터니언 – 인스펙터에서 게임오브젝트의 회전 값을 X: 0, Y: 365, Z: 0 으로 입력했을 때 이 값을 쿼터니언으로는 표현할 수 없으므로 재생을 누르면 오브젝트의 회전값이 X: 0, Y: 5, Z: 0(또는 기타 유사한 값)으로 변경되는 부작용이 있다. ‘360도 전체 회전 더하기 5도’라는 개념을 이해하지 못하고 단순히 회전 결과와 동일한 방법으로 회전하도록 설정된 쿼터니언으로 변환되기 때문이다 – 스크립트에서 회전을 처리하는 경우 Quaternion 클래스와 이 클래스의 메서드를 이용해 회전 값을 만들고 수정해야 한다. 오일러 각을 관장하는 Quaternion 클래스 메서드가 있기에 오일러 각을 사용할 수도 있지만, 의도하지 않은 부작용이 발생할 수 있기에 정확한 원리를 알고 조작해야 한다. ex) 쿼터니언을 통해 오일러 값에 접근해서 수정한 후 다시 쿼터니언으로 변환해서 적용하면 문제가 발생한다. 따라서 오일러 각 관련 메서드는 값을 받아와서 수정하지 않고 바로 적용하는 방식으로만 사용해야 한다 – 180도가 넘는 회전이 일어날 때 쿼터니언의 특성에 유의해야 한다 (참고: https://stackoverflow.com/questions/50311059/unity-rotate-an-object-in-axis-and-back-to-starting-point-in-the-same-direction 임의의 회전 순서 설정 – 오일러 각은 세 개의 축을 어떤 순서로 회전시키는지에 따라 결과가 달라진다(아래 그림 참고) – 유니티의 오일러 각 회전 순서는 Z, X, Y축 순이다(마야는 Z, Y, X축 순) 출처: https://vimeo.com/2649637 – 스크립트를 통해 회전 순서를 임의로 정할 수 있다(아래 코드 참고) – Transform.Rotate 메서드(벡터 인수)를 이용한 회전은 특정 축을 회전시키면 나머지 축들도 함께 회전하는 로컬 좌표축을 기준으로 계산된다. 따라서 회전이 Z, X, Y축 순으로 적용되는 일반적인 유니티 환경에서 맨 처음 Z축을 기준으로 회전하면 X, Y축도 같이 회전한다. 회전한 X축을 기준으로 두 번째 회전이 일어나며 이때 Y축도 같이 회전한다. 마지막으로 Y축을 기준으로 세 번째 회전이 일어나며 이때 같이 회전하는 축은 없다(로컬 좌표축 기즈모를 기준으로 생각하면 헷갈릴 수 있다. 왜냐면 기즈모는 하나의 축이 변화할 때 항상 나머지 두 개의 축도 같이 회전하기 때문이다. 그러나 오일러 각은 하나의 축이 회전할 때 아직 회전하지 않은 축만 같이 회전한다) – 만약 변하지 않고 고정된 축을 기준으로 계속 회전을 일으키고 싶은 경우에는 parent 와 Transform.RotateAround 메서드를 활용한다(아래 코드 참고) – Quaternion 연산에서 곱셈의 의미: Quaternion A, B 가 있을 때 (A * B) 는 우선 B 만큼의 회전량을 적용한 후 이어서 A만큼의 회전량을 적용한다는 의미이다 – Rotate, RotateAround 메서드에 대한 정보는 다음 게시글 참고(https://blog.naver.com/dj3630/221447290180) //두 쿼터니언의 회전량을 더하는 방법(곱셈 연산) Quaternion originalRotation = Quaternion.Euler(new Vector3(45, 0, 0)); Quaternion plusRotation = Quaternion.Euler(new Vector3(40, 0, 0)); Quaternion targetRotation = originalRotation * plusRotation; transform.rotation = targetRotation; //X축-Y축-Z축 순서로 회전하게 만들기 //올바른 예: 원하는 회전순서의 역순으로 쿼터니언(회전량)을 서로 곱해준다 //단, 매 회전 마다 고정된 글로벌 좌표축을 기준으로 회전량 계산 transform.localRotation = Quaternion.AngleAxis(angleZ, Vector3.forward) * Quaternion.AngleAxis(angleY, Vector3.up) * Quaternion.AngleAxis(angleX, Vector3.right); //올바른 예: RotateAround 메서드 이용 //단, 매 회전 마다 고정된 특정 좌표축을 기준으로 회전량 계산 Transform par = transform.parent.transform; transform.rotation = Quaternion.Identity; transform.RotateAround(transform.position, par.right, rotation.x); transform.RotateAround(transform.position, par.up, rotation.y); transform.RotateAround(transform.position, par.forward, rotation.z); //올바른 예: Rotate 메서드 이용 //단, 매 회전 마다 변화하는 로컬 좌표축을 기준으로 회전량 계산 transform.Rotate(angleX, 0, 0); transform.Rotate(0, angleY, 0); transform.Rotate(0, 0, angleZ); //잘못된 예: 회전순서에 영향을 주지 않는다 //단, 매 회전 마다 변화하는 로컬 좌표축을 기준으로 회전량 계산 Transform.Rotate(new Vector3(a, b, c)); //잘못된 예: 맨 마지막 코드 한 줄만 최종적으로 적용되기에 선행하는 코드 두 줄은 무시된다(=회전이 중첩되지 않는다) //즉, 회전순서에 영향을 주지 않는다 transform.localRotation = Quaternion.AngleAxis(angleX, Vector3.right); transform.localRotation = Quaternion.AngleAxis(angleY, Vector3.up); transform.localRotation = Quaternion.AngleAxis(angleZ, Vector3.forward); //잘못된 예: eulerAngles 속성의 x, y, z 는 직접 변경(set)할 수 없다 transform.eulerAngles.x = angleX; transform.eulerAngles.y = angleY; transform.eulerAngles.z = angleZ; //잘못된 예: eulerAngles 속성에 값 대입을 통한 회전은 에디터 상의 rotation 값에 직접 대입되는 방식으로 적용된다 //즉, 회전은 중첩되지만 유니티 기본 회전순서에 영향을 주지 않는다 transform.eulerAngles = new Vector3(angleX, transform.eulerAngles.y, transform.eulerAngles.z); transform.eulerAngles = new Vector3(transform.eulerAngles.x, angleY, transform.eulerAngles.z); transform.eulerAngles = new Vector3(transform.eulerAngles.x, transform.eulerAngles.y, angleZ); 쿼터니언 활용법 //쿼터니언 사용시 유의사항 //올바른 예: 오일러 각을 쿼터니언으로 변환하여 회전 제어 float x; x += Time.deltaTime * 10; transform.rotation = Quaternion.Euler(x,0,0); //잘못된 예: 쿼터니언의 성분을 직접 조작해서는 원하는 결과를 얻기 힘들다(쿼터니언 수학을 완전히 이해해야만 제대로 조작할 수 있다) var rot = transform.rotation; rot.x += Time.deltaTime * 10; transform.rotation = rot; //잘못된 예: 쿼터니언을 오일러 각으로 변환해서 조작한 후 다시 쿼터니언으로 변환한 경우 오작동을 일으킬 가능성이 높다 var angles = transform.rotation.eulerAngles; angles.x += Time.deltaTime * 10; transform.rotation = Quaternion.Euler(angles); //특정 축을 기준으로 한 회전량(X축 10도) 계산 Quaternion rotR = Quaternion.AngleAxis(10, Vector3.right); //로컬 X축을 기준으로 10도 만큼 회전 transform.Rotate(Vector3.right * 10); //방법 1 transform.Rotate(10, 0, 0); //방법 2 transform.rotation = transform.rotation * rotR; //방법 3 transform.localRotation = Quaternion.Euler(0, 10, 0); //잘못된 방법: 오브젝트의 기존 회전 상태에 더해지는 게 아니라 identity 를 기준으로 오일러 각 회전 대입 transform.localRotation = rotR; //잘못된 방법: 오브젝트의 기존 회전 상태에 더해지는 게 아니라 identity 를 기준으로 회전량 대입 //글로벌 X축을 기준으로 10도 만큼 회전 transform.Rotate(Vector3.right * 10, Space.World); //방법 1 transform.Rotate(10, 0, 0, Space.World); //방법 2 transform.rotation = rotR * transform.rotation; //방법 3 transform.rotation = Quaternion.Euler(0, 10, 0); //잘못된 방법: 오브젝트의 기존 회전 상태에 더해지는 게 아니라 identity 를 기준으로 오일러 각 회전 대입 transform.rotation = rotR; //잘못된 방법: 오브젝트의 기존 회전 상태에 더해지는 게 아니라 identity 를 기준으로 회전량 대입 //쿼터니언을 이용해 원하는 방향을 가리키는 방법 public Transform targetTransform; Vector3 direction = targetTransform.position – transform.position; Quaternion targetRotation = Quaternion.LookRotation(direction); transform.rotation = targetRotation; //쿼터니언을 이용해 벡터를 회전시킬 수 있다(역은 성립하지 않는다) //캐릭터의 정면(로컬 Z축) 방향으로 뻗어나가는 CharacterForward 벡터 Vector3 CharacterForward = character.rotation * Vector3.forward; 참고 영상 Scripting API Quaternion 유니티에서 회전을 조작하는 구조체 public static Quaternion identity: 회전량이 0인 상태의 쿼터니언(0.0, 0.0, 0.0, 1.0). 다른 게임오브젝트에 child 되어 있지 않다면 글로벌 좌표축이 identity 가 되고 child 되어 있다면 parent의 회전 상태가 identity 가 된다(읽기전용) public Vector3 eulerAngles: 글로벌 좌표축 기준 쿼터니언 회전량을 오일러 각으로 반환하거나 오일러각으로 쿼터니언을 조작(set)할 수 있게 해주는 속성. 이 때 오일러 각의 회전은 Z, X, Y 순으로 적용된다 public static Quaternion FromToRotation(Vector3 fromDirection, Vector3 toDirection) – 첫 번째 인수의 방향(orientation)에서 두 번째 인수의 방향까지의 회전값 차이를 쿼터니언으로 반환한다 public static Quaternion LookRotation(Vector3 forward, Vector3 upwards = Vector3.up) – 첫 번째 인수로 바라보고자 하는 지점(글로벌 좌표)을 전달하고 두 번째 인수로 기준이 될 up을 전달한다 – 메서드를 호출한 게임오브젝트의 로컬 Z축이 첫 번째 인수를 향하도록 회전시킨 후 로컬 Y축이 두 전째 인수를 향하도록 다시 회전시킨다 – 첫 번째 또는 두 번째 인수의 크기가 0인 경우 또는 첫 번째와 두 번째 인수가 서로 평행하는 벡터인 경우 identity 반환 – Transform.LookAt 메서드와 기능이 같다 //타겟을 향하도록 회전시키는 로직 public Transform target; void Update() { //LookRotation 메서드 이용 Vector3 relativePos = target.position – transform.position; Quaternion rotation = Quaternion.LookRotation(relativePos, Vector3.up); transform.rotation = rotation; //LookAt 메서드 이용 //transform.LookAt(target, Vector3.up); //transform.LookAt(target.position, Vector3.up); } public static float Angle(Quaternion a, Quaternion b) – 두 쿼터니언 사이의 각도 차이를 0.0F~ 180.0F 사이의 실수값으로 반환 public static Quaternion AngleAxis(float angle, Vector3 axis) – 인수로 전달한 각도와 축을 기준으로 한 회전량을 쿼터니언으로 변환하여 반환 – 두 번째 인수는 로컬 좌표축 기반(?) public static Quaternion Euler(float x, float y, float z) public static Quaternion Euler(Vector3 euler) – 오일러 각의 회전값을 쿼터니언으로 변환하여 반환 public static Quaternion Lerp(Quaternion a, Quaternion b, float t) – 0.0~1.0의 값이 가지는 t에 따라 두 회전상태를 직선 보간한다(t에 따른 변화량이 일정하다) – Slerp에 비해 속도는 빠르지만 두 회전상태의 차이가 크다면 보기에 안 좋다 public static Quaternion Slerp(Quaternion a, Quaternion b, float t) – 0.0~1.0의 값이 가지는 t에 따라 두 회전상태를 t에 따라 원형 보간한다(t에 따른 변화량이 다르다. 0.0과 1.0 근처에서 느리게 변한다) [개념정리] *Quaternion 을 통한 회전(스크립트 이용)은 기본적으로 Quaternion.identity 를 기준으로 적용된다. 즉, 글로벌 좌표축(child 상태 아닐 때) 또는 parent 의 로컬 좌표축(child 상태일 때) 을 기준으로 회전량을 적용하는 것이지, child 게임오브젝트의 회전 상태(localRotation)와는 무관하다. 단, 쿼터니언의 곱셈 연산의 경우 회전량이 서로 더해진다 ex) child 게임오브젝트의 인스펙터 뷰에 rotation 값이 (10, 20, 30)으로 설정되어 있다고 가정하자. 이때 Quaternion.AngleAxis 메서드로 계산한 회전량을 localRotation 에 대입해서 게임오브젝트를 회전시키는 코드를 작성했다면, 기존의 localRotation (10, 20, 30)은 코드를 통한 회전에 영향을 주지 않는다 ex) 쿼터니언 A, B, C 에 대해 (A*B*C) 의 회전량: 우선 identity 를 기준으로 C 만큼 회전하고 이어서 현재의 회전 상태를 기준으로 B 만큼 회전 한 후 마지막으로 B * C 만큼의 회전 상태를 기준으로 A 만큼 회전한다 *Quaternion 클래스의 메서드에서 회전량을 계산할 때는 회전하지 않은 상태, 즉 Quaternion.identity 를 기준으로 얼마나 회전하는지를 구하는 것이다. ex) Quaternion.AngleAxis(50, Vector3.up) 은 Quaternion.identity 상태에서의 Y축을 기준으로 50도 만큼 회전하는 회전량을 반환한다 *씬 뷰의 기즈모를 통한 회전은 사용자 편의를 위한 것이기에 기즈모의 특정 축을 잡고 돌리면 실제로 그 형태가 되기 위해 필요한 회전 값이 계산되어 인스펙터 뷰의 rotation 에 나타난다. 이때 원래 회전 상태(identity)를 기준으로 여러 축 회전이 동시에 일어나야 하는 경우 rotation 에서 두 개 이상의 값이 동시에 변하기도 한다. 마찬가지로 회전 기즈모의 X축을 잡고 회전시킨다고 해서 identity 기준 X축 회전만 일어나는 게 아니기에 인스펙터 뷰에서는 X값 이외에 Y, Z값도 함께 변할 수 있다 *오브젝트를 글로벌 좌표축 기준으로 회전시킬 때(=localRotation 이 아니라 rotation 을 제어할 때) 축의 원점을 자기 자신의 pivot에 두고 회전을 판단하면 된다. 다시 말해, 오브젝트가 이동하면서 position이 글로벌 좌표축의 원점(0, 0, 0)과 달라지는 경우 position의 기준이 되는 글로벌 좌표축은 여전히 3D공간의 원점을 기준으로 삼지만, rotation의 기준이 되는 글로벌 좌표축은 오브젝트와 동일한 만큼 이동해서 오브젝트의 pivot에 위치하는 것으로 생각하면 편하다 *오일러 각의 X, Y, Z 성분과 쿼터니언의 X, Y, Z 성분은 완전히 다르다. 즉, 오일러 각(50, 50, 50)을 쿼터니언으로 변환했을 때 그 값이 (50, 50, 50, w)가 아니다. 오일러 각과 쿼터니언의 상관관계는 다음 사이트 참고(https://quaternions.online/) *게임오브젝트 회전의 기준점은 Center 가 아니라 Pivot 이다 *인스펙터 뷰에 나타나는 position, rotation, scale은 parent를 기준으로 삼았을 때의 상대적인 값이기에 엄밀히 말하면 local- 이 생략된 것이다 <참고자료> – 이재현, <절대강좌! 유니티>, 2018 – https://docs.unity3d.com/kr/2018.2/Manual/QuaternionAndEulerRotationsInUnity.html – https://docs.unity3d.com/ScriptReference/Quaternion.html – https://pxkey.blog.me/221389715050 – https://blog.naver.com/kimsung4752/221362786233 – https://www.youtube.com/watch?time_continue=45&v=uNHIPVOnt-Y – https://blog.naver.com/han95173/130157074226 – https://blog.naver.com/bestian/10073454337 – https://blog.naver.com/qkfkf123/60170135935 – https://www.youtube.com/watch?v=zc8b2Jo7mno – https://vimeo.com/2649637 – https://terms.naver.com/entry.nhn?docId=3571563&cid=58944&categoryId=5 – https://www.youtube.com/watch?v=jlskQDR8-bY – https://forum.unity.com/threads/understanding-rotations-in-local-and-world-space-quaternions.153330/ – https://blog.naver.com/mssixx/150143137018 – https://software.intel.com/en-us/forums/realsense/topic/562273 – https://stackoverflow.com/questions/50311059/unity-rotate-an-object-in-axis-and-back-to-starting-point-in-the-same-direction – https://gamedev.stackexchange.com/questions/147939/unity-rotate-object-around-local-x-axis-then-local-y-axis-then-local-z-axis – https://answers.unity.com/questions/977027/problem-with-rotation-order-of-euler-angles-when-i.html – https://gamedev.stackexchange.com/questions/111479/quaternion-rotation-problems – https://forum.unity.com/threads/understanding-rotations-in-local-and-world-space-quaternions.153330/ – https://vimeo.com/2649637 인쇄

[유니티] Euler, Quaternion 오일러각 쿼터니언 총 정리

반응형
[Unity] Euler, Quaternion 오일러각(짐벌락) 쿼터니언에 대하여!

Unity의 Euler 각도는 x,y,z 3개 축을 기준으로 회전시키는 우리가 흔히 알고있는 각도계를 의미한다.

Euler Angle

이 각도계를 사용하면 우리 모두 삽질할 필요없이 아름답게 개발을 할 수 있을텐데,

왜 Queternion 같은게 생겨서 우리를 괴롭히는가,,,

그 이유는 Euler angle은 짐벌락(‘Gimbal-lock’) 이라는 문제가 있기 때문에 모든 각도 변환을 표현하는데 한계가 있기 때문이다.

그 한계점을 보완하여 생겨난 게 쿼터니언(Quaternion)이다.

짐벌락이란 무엇인가 .

우선 간단하게 설명하자면, 같은 방향으로 오브젝트의 두 회전 축이 겹치는 현상이다.

사진으로 간단하게 설명하겠다.

우선 !

다음 사진과 같이 x, y ,z 축을 가진 오브젝트가 있다고 해보자.

저 화살표가 가리키는 방향을 계속 유의하자.

이 오브젝트의 x(빨간축) 축을 90도 회전시켜보겠다.

x축(빨간축)으로 90도 회전시킨 모습이다.

화살표를 보면 오른쪽 방향을 가리키고 있다.

여기까지는 문제가 없다.

자, 그다음 Y축(초록색)으로 90도 회전시켜보겠다.

Y축으로 90도 회전시키니 다음과 같은 모습이 된다.

Z 축과 X 축이 한축으로 합쳐지면서 한축에 대한 계산이 불가능해집니다.

이러한 현상을 바로 ‘짐벌락(Gimbal-lock)’ 이라고 한다.

이러한 짐벌락 현상이 생기는 이유는

오일러 앵글이 자체적으로 설정되어있는 순서로 해당 축들을 개별적으로 계산하기 때문이다.

Unity에서는 오일러 앵글이 X, Y, Z 순서로 계산된다.

세 개의 축을 동시에 계산하지 않고 각 축을 독립적으로 판단하기에 다음과 같이 어쩌다가 겹쳐버리는 현상이 발생하는 것이다.

이렇게 축이 겹쳐버리면 한 축에 대해서는 계산이 불가능하기에, 정확한 각도 계산이 불가능하다.

Unity로 2D 게임을 제작할 때는 오일러 각으로도 각도 구현에 문제가 없지만,

모든 각도를 통제해줘야 하는 3D 게임 같은 경우에는 오일러 앵글만으로는 구현에 한계가 있다.

오일러 각의 이러한 문제를 해결하기 위해 나온 것이 바로 쿼터니언(Quaternion) 이다.

쿼터니언(Quaternion)

쿼터니언은 각 축을 한꺼번에 계산하기 때문에 짐벌락 문제가 발생하지 않는다.

Euler angle 과는 다르게 쿼터니언은 4개의 성분(x, y, z, w)으로 이루어져 있다.

해당 성분은 벡터(x, y, z)와 스칼라(w)를 의미한다.

쿼터니언은 내부가 수학적으로 복잡하게 구현되어있어 이를 제대로 이해하지 못한다면 자유자재로 다루기는 상당히 까다롭다.

쿼터니언은 방향(orientation)과 회전(rotation) 둘을 다 표현할 수 있다.

하지만 쿼터니언의 회전은 한 orientation 에서 다른 orientation 으로 측정하기에 180 보다 큰 값을 표현할 수 없다는 단점이 있다.

이 점이 쿼터니언을 직관적으로 이해할 수 없는 큰 이유 중 하나이다.

다행히 유니티에는 이러한 쿼터니언을 간단하게 사용 가능하도록 만들어진 함수들이 다양하게 존재한다.

유니티 공식 문서에도 쿼터니언은 쓰기 어려우니 자기들이 만든 함수를 사용하도록 권장한다.

쿼터니언을 다루기 위해 사용되는 대표적인 함수들의 사용법을 정리해봤다.

Quaternion.Euler

public static Quaternion Euler(float x, float y, float z);

유니티에서는 Quaternion.Euler 함수를 통해서 오일러각을 쿼터니언으로 변경시켜 사용한다.

해당 함수 인자에 오일러각을 넣으면 쿼터니언으로 변환된 값을 반환시켜준다.

Euler 함수 사용법

transform.roation = Quaternion.Euler(new Vector3(120,60,100));

float x; void Update () { x += Time.deltaTime * 10; transform.rotation = Quaternion.Euler(x,0,0); }

Quaternion.LookRotation

public static Quaternion LookRotation(Vector3 forward, Vector3 upwards = Vector3.up);

두 번째 인자인 upwards upwards는 Vector3.up 으로 디폴트 인자가 세팅되어 있다.

첫 번째 인자에 방향벡터를 입력하면 해당 자기 위치기준에서의 해당 방향벡터를 바라보게 된다.

어떠한 타겟을 향해 회전시키고 싶다면 다음과 같이 사용하면 된다.

Vector3 direction = (traget.position – this.transform.position).normalized; Quaternion lookRotation = Quaternion.LookRotation(direction); this.transform.rotation = lookRotation;

Quaternion.Slerp

public static Quaternion Slerp(Quaternion a, Quaternion b, float t);

/from/과 /to/사이를 /t/로 구형보간 합니다.

Quaternion.Slerp 함수는 두 쿼터니언의 중간값을 리턴 시켜준다.

Slerp 함수를 사용할 때 종종 세 번째 인자인 t 값에 대하여 헷갈리는데,

Slerp 함수는 lerp 함수에서 쓰이는 선형보간법이 아닌 구면선형보간법 기반으로 되있다는 점을 명심해야한다.

Lerp 함수와 Slerp 함수는 세 번째 인자에 따른 반환값이 다르다.

Slerp를사용하고 싶다면 선형보간법과 구면선형보간법의 차이를 숙지해야 원하는 각도 변환을 연출할 수 있을 것이다.

Lerp, Slerp 차이.

Lerp와 Slerp의 차이를 간단하게 그림으로 나타내면 다음과 같다.

초록점에서 빨간 점으로 이동할 때 Lerp는 직선으로 Slerp는 곡선으로 보간 된다.

transform.rotation = Quaternion.Slerp(A.transform.rotation, B.transform.rotation, Time.deltaTime);

Quaternion.FromToRotation

public static Quaternion FromToRotation(Vector3 fromDirection, Vector3 toDirection);

/fromDirection/에서 /toDirection/으로 회전한 rotation을 생성합니다.

FromToRotaion 함수는 fromDirection 의 방향벡터를 toDirection 으로 회전한 쿼터니언을 반환한다.

rotation(0,0,0)

rotation 값이 (0,0,0)인인 큐브이다.

transform.rotation = Quaternion.FromToRotation(Vector3.up, Vector3.right);

다음 함수를 적용 시키면

큐브의 up vector(초록색 화살표)가 옆으로 꺽여있다.

카메라 위치 때문에 반대로 보이지만 큐브가 오른쪽으로 90도 회전한 모습이다.

FromToRotation 함수는 중심축을 첫 번째 인자로 넣고 회전하고 싶은 방향벡터를 두 번째 인자로 넣어서 사용하면 될듯싶다.

반응형

유니티 – 쿼터니언과 회전의 덧셈 (How to Add Two Quaternions)

728×90

반응형

Unity 전체 링크

유니티의 회전은 쿼터니언을 이용해야 한다.

인스펙터의 Rotation은 Vector3로 표현되지만 실제 타입은 Quaternion이다.

유니티가 사용자에게 보기 좋게 Vector3로 변환해 준 것이다.

Rotation은 Vector3가 아니기 때문에 Quaternion.Euler(Vector3)로 변환해야 한다.

그리고 Rotation의 값을 얻기 위해서는 rotation의 eulerAngles로 접근한다.

먼저 QuaternionTest.cs를 추가해보자.

실제 Rotation은 Vector3가 아니기 때문에 Quaternion.Euler(Vector3)로 변환한다.

using System.Collections; using System.Collections.Generic; using UnityEngine; public class QuaternionTest : MonoBehaviour { void Start() { Quaternion rotation = Quaternion.Euler(new Vector3(45, 45, 0)); this.transform.rotation = rotation; Debug.Log(“rotation : ” + this.transform.rotation); Debug.Log(“Quaternion : ” + this.transform.rotation.eulerAngles); } }

아래의 그림과 같은 결과가 나온다.

로그를 보면, 실제 Inspector에 있는 Rotation은 eulerAngles로 접근해야 하는 것을 알 수 있다.

이제 회전을 더해보자.

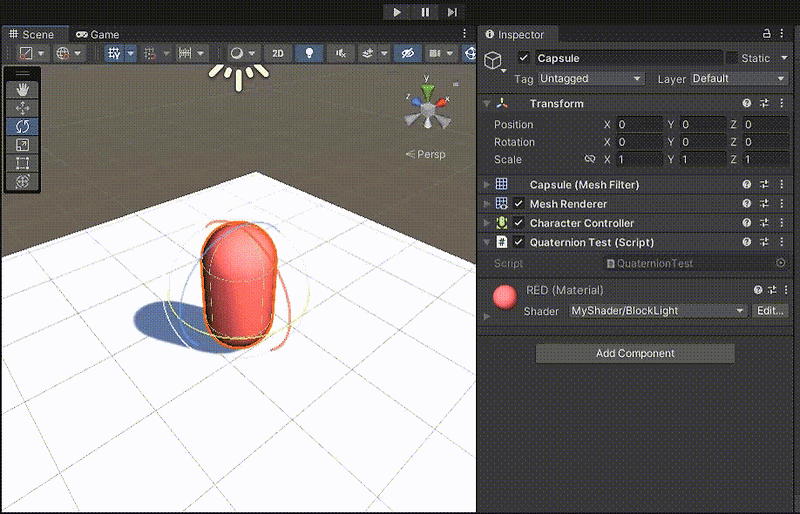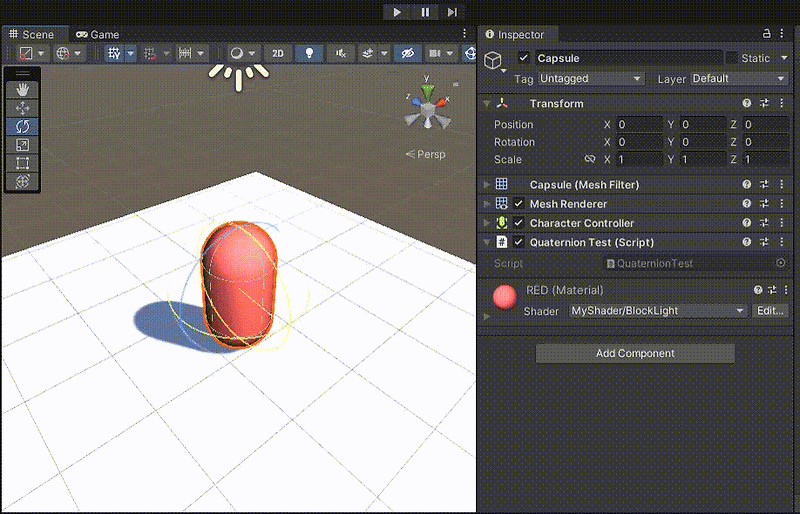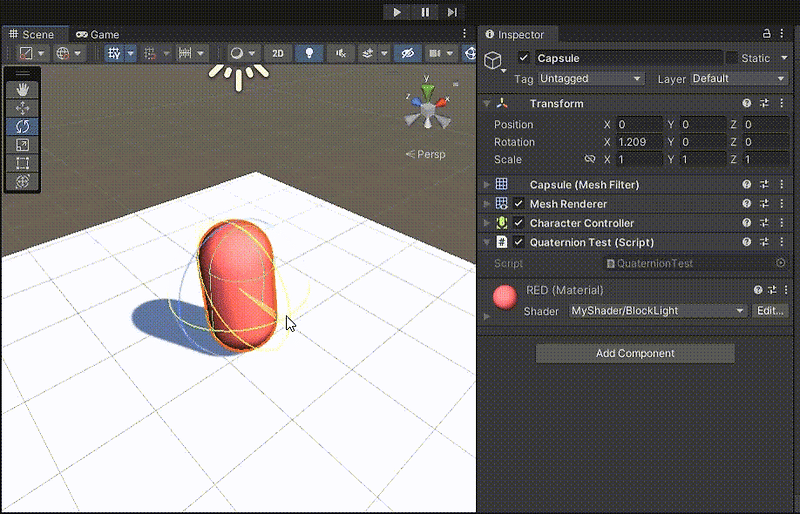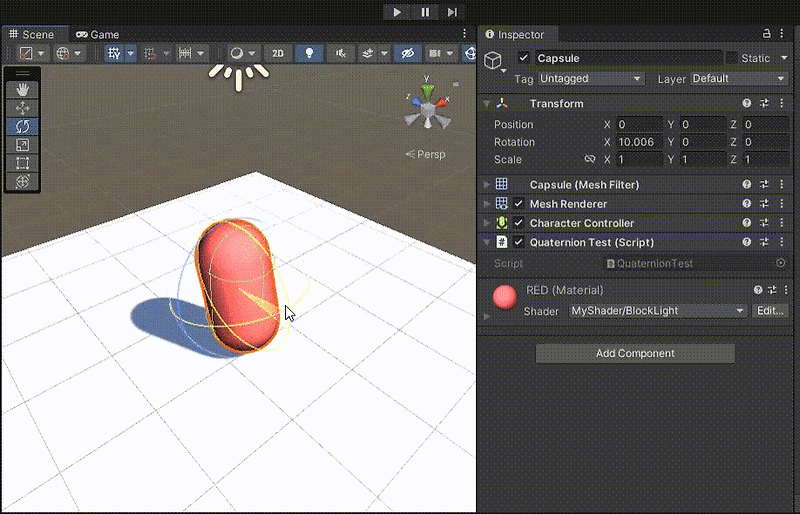
먼저 Scene에서 X축으로 45도 회전한 후, Y축으로 45도 회전해보자.

Scene에서 마우스로 이동하기 때문에 정확히 45도로 맞추지 않고,

아래와 같이 호의 넓이로 적당히 어림짐작한다.

X축으로 45도 회전한 후, Y축으로 45도 회전하였다.

Rotation의 결과는 약 (45, 45, 0)이 된다.

이제 Y축으로 45도 회전하고, X축으로 45도 회전해보자.

결과는 약 (30, 55, 36)으로 (45, 45, 0) 이 나오지 않는 것을 알 수 있다.

두 결과를 비교하면 아래와 같다.

X를 먼저 45º 회전하고, Y를 45º 회전하는 경우 (43.5, 47.3 , 0) → 정확히 회전한 경우 : (45, 45, 0)

Y를 먼저 45º 회전하고, X를 45º 회전하는 경우 (30.3, 55.8 , 36.6) → 정확히 회전한 경우 : (30, 54.7, 35.2)

X -> Y vs Y -> X

회전은 축을 기준으로 하기 때문에 순서가 결과에 영향이 생긴다.

즉, 회전에서 X → Y ≠ Y → X 이다.

이제 수동으로 회전을 더하지 말고, 스크립트로 회전을 해보자.

아래와 같이 rotX, rotY를 정한 후, rotX → rotY와 rotY → rotX의 결과를 비교해보자.

참고로 쿼터니언을 더하면 컴파일 에러가 발생한다.

쿼터니언은 실제로 행렬 연산이기 때문에 곱셈 연산이 두 회전의 덧셈이다.

이제 코드를 수정하고 두 결과를 비교해보자.

using System.Collections; using System.Collections.Generic; using UnityEngine; public class QuaternionTest : MonoBehaviour { void Start() { Quaternion rotX = Quaternion.Euler(new Vector3(45, 0, 0)); Quaternion rotY = Quaternion.Euler(new Vector3(0, 45, 0)); this.transform.rotation = rotX * rotY; Vector3 X_Y = this.transform.rotation.eulerAngles; this.transform.rotation = rotY * rotX; Vector3 Y_X = this.transform.rotation.eulerAngles; Debug.Log(“First X -> Y rotation ” + X_Y); Debug.Log(“First Y -> X rotation ” + Y_X); } }

수동으로 회전한 X → Y는 (45, 45, 0)이었으나 rotX * rotY 의 결과는 (30, 54.7, 35.2)인 것을 알 수 있다.

마찬가지로 수동 회전 Y → X는 (30, 54.7, 35.2)였지만, 결과는 (45, 45, 0)이다.

즉, X로 먼저 회전하고 싶다면 뒤에서 곱해야하는 것을 알 수 있다.

실제 올바른 코드는 아래와 같다.

using System.Collections; using System.Collections.Generic; using UnityEngine; public class QuaternionTest : MonoBehaviour { void Start() { Quaternion rotX = Quaternion.Euler(new Vector3(45, 0, 0)); Quaternion rotY = Quaternion.Euler(new Vector3(0, 45, 0)); this.transform.rotation = rotY * rotX; // X 먼저 회전 후, Y 회전 Vector3 X_Y = this.transform.rotation.eulerAngles; this.transform.rotation = rotX * rotY; // Y 먼저 회전 후, X 회전 Vector3 Y_X = this.transform.rotation.eulerAngles; Debug.Log(“First X -> Y rotation ” + X_Y); Debug.Log(“First Y -> X rotation ” + Y_X); } }

따라서 회전에서 X → Y ≠ Y → X이고 연산에서 X를 먼저 회전하기 위해서는 뒤에 곱해야 한다.

728×90

반응형

So you have finished reading the 유니티 quaternion 연산 topic article, if you find this article useful, please share it. Thank you very much. See more: 유니티 각도만큼 회전, Quaternion, 유니티 Quaternion, Quaternion Euler, Quaternion angle, Quaternion rotation, 유니티 회전 범위, 유니티 eulerAngles

Top 45 유니티 Quaternion 연산 The 195 Detailed Answer

[유니티 기초] – Quaternion : 네이버 블로그

유니티 – Quaternion | Rito15

[유니티] Euler, Quaternion 오일러각 쿼터니언 총 정리

유니티 – 쿼터니언과 회전의 덧셈 (How to Add Two Quaternions)

(유니티) 회전(rotation)과 쿼터니언 – 앤글 블로그

쿼터니언(사원수), Quaternions

쿼터니온(Quaternion) 정리

[Unity3D] 오브젝트 회전 – Quaternion

[유니티 기초] – Quaternion

[유니티] Euler, Quaternion 오일러각 쿼터니언 총 정리

유니티 – 쿼터니언과 회전의 덧셈 (How to Add Two Quaternions)

Leave a Comment Cancel reply