You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 파이썬 회귀 분석 on Google, you do not find the information you need! Here are the best content compiled and compiled by the toplist.Experience-Porthcawl.com team, along with other related topics such as: 파이썬 회귀 분석 파이썬 sklearn 회귀분석, 파이썬 다중회귀분석, 파이썬 회귀분석 예제, 파이썬 회귀분석 코드, 파이썬 선형회귀분석, 파이썬 회귀분석 그래프, 파이썬 단순회귀분석, 파이썬 회귀분석 시각화
[Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악]
- Article author: ordo.tistory.com
- Reviews from users: 13151
Ratings
- Top rated: 3.6
- Lowest rated: 1
- Summary of article content: Articles about [Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악] [Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악]. JKyun 2021. 8. 7. 19:02. 안녕하세요~ 우주신 입니다. 저번 상관분석 포스팅에 … …
- Most searched keywords: Whether you are looking for [Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악] [Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악]. JKyun 2021. 8. 7. 19:02. 안녕하세요~ 우주신 입니다. 저번 상관분석 포스팅에 … 안녕하세요~ 우주신 입니다. 저번 상관분석 포스팅에 이어 이번에는 회귀분석(Regression Analysis)에 대해 정리 해보겠습니다. 상관분석은 변수들이 서로 얼마나 밀접하게 직선적인 관계를 가지고 있는지를 분석..
- Table of Contents:
태그
관련글
댓글2
공지사항
최근글
인기글
최근댓글
태그
전체 방문자
![[Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악]](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbOph0N%2Fbtrboss4Wdn%2Ft2SxjXqGZ9XWKwLXMOs9J0%2Fimg.png)
회귀분석 실시하기 :: Python 기초 통계 :: 마인드스케일
- Article author: mindscale.kr
- Reviews from users: 49979
Ratings
- Top rated: 3.6
- Lowest rated: 1
- Summary of article content: Articles about 회귀분석 실시하기 :: Python 기초 통계 :: 마인드스케일 Python 기초 통계 … ols 함수로 회귀분석을 실시한다. … 독립변수가 여러 개인 다중회귀분석에서 사용; 독립변수의 개수와 표본의 크기를 고려 … …
- Most searched keywords: Whether you are looking for 회귀분석 실시하기 :: Python 기초 통계 :: 마인드스케일 Python 기초 통계 … ols 함수로 회귀분석을 실시한다. … 독립변수가 여러 개인 다중회귀분석에서 사용; 독립변수의 개수와 표본의 크기를 고려 …
- Table of Contents:
Python 기초 통계
명수강중
예제 데이터 준비
회귀분석 실시
목차

4.1 회귀분석 예제 — 데이터 사이언스 스쿨
- Article author: datascienceschool.net
- Reviews from users: 38206
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about 4.1 회귀분석 예제 — 데이터 사이언스 스쿨 예측문제 중에서 출력변수의 값이 연속값인 문제를 회귀(regression) 또는 회귀분석(regression analysis) 문제라고 한다. 이 절에서는 회귀분석의 몇가지 예를 들어 … …
- Most searched keywords: Whether you are looking for 4.1 회귀분석 예제 — 데이터 사이언스 스쿨 예측문제 중에서 출력변수의 값이 연속값인 문제를 회귀(regression) 또는 회귀분석(regression analysis) 문제라고 한다. 이 절에서는 회귀분석의 몇가지 예를 들어 …
- Table of Contents:
보스턴 집값 예측¶
당뇨병 진행도 예측¶
가상 데이터 예측¶

[Python] 머신러닝 – 회귀분석(단순회귀분석, 다항회귀분석, 다중회귀분석) : 네이버 블로그
- Article author: blog.naver.com
- Reviews from users: 40500
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about [Python] 머신러닝 – 회귀분석(단순회귀분석, 다항회귀분석, 다중회귀분석) : 네이버 블로그 머신러닝. . 1. 종류. – 지도학습 : 정답을 알고 학습( 예측 : 회귀분석, 분류 : KNN). – 비지도학습 : 정답이 없는 상태에서 서로 비슷한 데이터 … …
- Most searched keywords: Whether you are looking for [Python] 머신러닝 – 회귀분석(단순회귀분석, 다항회귀분석, 다중회귀분석) : 네이버 블로그 머신러닝. . 1. 종류. – 지도학습 : 정답을 알고 학습( 예측 : 회귀분석, 분류 : KNN). – 비지도학습 : 정답이 없는 상태에서 서로 비슷한 데이터 …
- Table of Contents:
악성코드가 포함되어 있는 파일입니다
작성자 이외의 방문자에게는 이용이 제한되었습니다
![[Python] 머신러닝 - 회귀분석(단순회귀분석, 다항회귀분석, 다중회귀분석) : 네이버 블로그](https://blogthumb.pstatic.net/MjAyMTA4MDFfMjk1/MDAxNjI3ODAyNjk3NDg3.Hnx6zrSNhzD4fvaT6gxCbj7cGWSBKosGcJRudkCeXfog.Pm3m4XBoVTNIH8JLNDTQ9QnYG9kmYfdDrWNd-u4XWbIg.PNG.lajy0313/Figure_8.png?type=w2)
[회귀 분석] 1. Python을 이용하여 단순 선형 회귀 모형 적합해보기!
- Article author: zephyrus1111.tistory.com
- Reviews from users: 15375
Ratings
- Top rated: 3.8
- Lowest rated: 1
- Summary of article content: Articles about [회귀 분석] 1. Python을 이용하여 단순 선형 회귀 모형 적합해보기! 회귀 분석은 관심이 대상이 되는 변수와 설명 변수들 간의 연관성을 파악하기 위한 분석으로써 많이 활용되고 있어요. 이번 포스팅에서는 Python을 … …
- Most searched keywords: Whether you are looking for [회귀 분석] 1. Python을 이용하여 단순 선형 회귀 모형 적합해보기! 회귀 분석은 관심이 대상이 되는 변수와 설명 변수들 간의 연관성을 파악하기 위한 분석으로써 많이 활용되고 있어요. 이번 포스팅에서는 Python을 … 안녕하세요~ 꽁냥이에요! 회귀 분석은 관심이 대상이 되는 변수와 설명 변수들 간의 연관성을 파악하기 위한 분석으로써 많이 활용되고 있어요. 이번 포스팅에서는 Python을 이용하여 단순 선형 회귀 모형을 적합..
- Table of Contents:
1 데이터 살펴보기
2 statsmodels 라이브러리를 이용하여 적합해보기
3 scikit-learn(sklearn)을 이용하여 적합하기
관련글
댓글0
전체 방문자
최근글
인기글
티스토리툴바
![[회귀 분석] 1. Python을 이용하여 단순 선형 회귀 모형 적합해보기!](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fz6ZRz%2FbtqIAP378qX%2FWLmvCh8DbiTEjMUWMnMhbk%2Fimg.png)
파이썬 데이터분석 회귀분석
- Article author: no17.tistory.com
- Reviews from users: 12852
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about 파이썬 데이터분석 회귀분석 오늘은 파이썬으로 단순회귀분석, 다중회귀분석을 시행해 보겠습니다. 개요. 회귀분석이란 수치형 종속변수와 수치형 독립변수사이의 영향 또는 인과 … …
- Most searched keywords: Whether you are looking for 파이썬 데이터분석 회귀분석 오늘은 파이썬으로 단순회귀분석, 다중회귀분석을 시행해 보겠습니다. 개요. 회귀분석이란 수치형 종속변수와 수치형 독립변수사이의 영향 또는 인과 … 안녕하세요. 오늘은 파이썬으로 단순회귀분석, 다중회귀분석을 시행해 보겠습니다. 개요 회귀분석이란 수치형 종속변수와 수치형 독립변수사이의 영향 또는 인과관계를 알 수 있는 분석이다. 언뜻 보면 상관관계..
- Table of Contents:
‘Data science for Marketing’ Related Articles
티스토리툴바

Python) 회귀 분석 기본 사용법 정리(scikit-learn, statsmodels)
- Article author: data-newbie.tistory.com
- Reviews from users: 15935
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about Python) 회귀 분석 기본 사용법 정리(scikit-learn, statsmodels) 파이썬에서 Linear Regression 하는 것에서 기본적인 것이 Scikit-Learn이 있는데, 통계분석을 같이 하고 싶다면 statsmodels 을 쓰는 것이 더 좋다. …
- Most searched keywords: Whether you are looking for Python) 회귀 분석 기본 사용법 정리(scikit-learn, statsmodels) 파이썬에서 Linear Regression 하는 것에서 기본적인 것이 Scikit-Learn이 있는데, 통계분석을 같이 하고 싶다면 statsmodels 을 쓰는 것이 더 좋다. 파이썬에서 Linear Regression 하는 것에서 기본적인 것이 Scikit-Learn이 있는데, 통계분석을 같이 하고 싶다면 statsmodels 을 쓰는 것이 더 좋다. 그래서 오랜만에 쓸 기회가 있어서 사용하다가 정리를 해봤다…R, Python 을 주로 사용하여 데이터 분석을 합니다.
https://github.com/sungreong - Table of Contents:
Library
연속형 변수
범주형 변수+ 연속형 변수
티스토리툴바
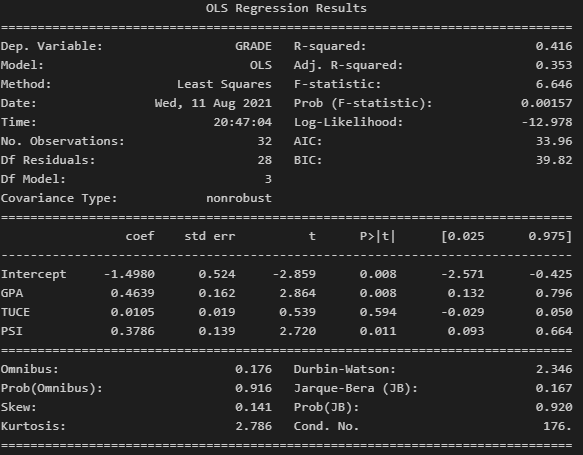
[Python Data Analysis 분석 6] 데이터 분석 – 파이썬 선형 회귀분석(1/2)
- Article author: tjansry354.tistory.com
- Reviews from users: 27874
Ratings
- Top rated: 4.8
- Lowest rated: 1
- Summary of article content: Articles about [Python Data Analysis 분석 6] 데이터 분석 – 파이썬 선형 회귀분석(1/2) 네이버 블로그로 이전했습니다. https://blog.naver.com/moongda0404/222729519749 [Python Data Analysis 분석 6] 데이터 분석 – 파이썬 선형 회귀 … …
- Most searched keywords: Whether you are looking for [Python Data Analysis 분석 6] 데이터 분석 – 파이썬 선형 회귀분석(1/2) 네이버 블로그로 이전했습니다. https://blog.naver.com/moongda0404/222729519749 [Python Data Analysis 분석 6] 데이터 분석 – 파이썬 선형 회귀 … 네이버 블로그로 이전했습니다. https://blog.naver.com/moongda0404/222729519749 [Python Data Analysis 분석 6] 데이터 분석 – 파이썬 선형 회귀분석(1/2) *본 글은 Python3을 이용한 데이터 분석(Data Analysi..
- Table of Contents:
태그
관련글
댓글5
공지사항
최근글
인기글
최근댓글
태그
전체 방문자
티스토리툴바
![[Python Data Analysis 분석 6] 데이터 분석 - 파이썬 선형 회귀분석(1/2)](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FlF5x6%2FbtqETmRf69w%2FxKUukzaLhD9GGO6HlIP1Q1%2Fimg.png)
See more articles in the same category here: toplist.Experience-Porthcawl.com/blog.
[Python] 회귀분석(Regression Analysis) [회귀식 추정, 회귀모형 검정, 적합도 파악]
안녕하세요~ 우주신 입니다.
저번 상관분석 포스팅에 이어 이번에는 회귀분석(Regression Analysis)에 대해 정리 해보겠습니다.
상관분석은 변수들이 서로 얼마나 밀접하게 직선적인 관계를 가지고 있는지를 분석하는 통계적 기법이며,
(바로 이전 글에 자세히 다뤄봤으니 참고)
회귀분석은 한 개 또는 그 이상의 변수들(독립변수)에 대하여 다른 변수(종속변수) 사이의 관계를
수학적인 모형을 이용하여 설명하고 예측하는 분석기법 입니다.
쉽게 말하자면, 상관분석에서는 산점도의 점들의 분포를 통해 일정한 패턴을 확인한 후,
상관계수를 구하여 두 변수 간의 선형 관계를 알 수 있었습니다.
여기서 더 나아가, 이 일정한 패턴을 활용하여 무엇인가를 예측하는 분석을 회귀분석이라고 보시면 됩니다.
회귀분석 하면 괜히 이름도 생소하고 낯설 수 있지만, 코드와 함께 따라가보시죠.
상관분석의 연장선에서 설명하고자 회귀분석에서도 같은 데이터를 사용하겠습니다.
이번 예시에서는 당뇨와 그에 영향을 미치는 변수들 간의 관계를 분석해 보죠.
먼저 데이터는 sklearn에서 제공하는 datasets을 불러왔습니다.
import pandas as pd import numpy as np from sklearn import datasets data = datsets.load_diabetes()
데이터가 dictionary 형태이므로 어떤 key를 가지는지 확인해보면 아래와 같이 나오고,
여기서 data, target, feature_names 세 가지 key만 쓰겠습니다. 당연히 데이터 형태의 길이가 같은지 부터 확인해야죠.
여기서 target이 당뇨병의 수치이고 나머지 feature names에 속하는 age, sex, bmi 등등은 변수라고 보면 됩니다.
즉, 442명의 사람들을 상대로 10가지의 특성들을 나열한거죠.
저번 포스팅의 상관분석을 통해 당뇨병의 수치(target)와 bmi(체질량지수) 간의 일정한 패턴을 확인하였고, 상관계수 또한 0.59로써 양의 선형관계를 이뤘습니다. 여기서 더 나아가, 회귀분석을 통해 변수 간에 관계를 예측해보죠.
회귀분석은 크게 독립변수 종속변수가 각각 한 개일 때의 관계를 분석하는 단순선형회귀분석(simple linear regression analysis)과 종속변수는 한개 독립변수는 두개 이상일 때는 중선형회귀분석(multiple linear regression analysis)으로 구분 됩니다.
<단순선형회귀분석>
1. 회귀식의 추정
두 변수 X와 Y의 관계(bmi, target)에 적합한 회귀식을 구하기 위해서는 관측된 값으로부터 회귀계수 B0와 B1의 값을 추정하여야 합니다.
이 때 일반적으로 많이 사용되는 방법을 최소제곱법이라고 합니다.
여러가지 방법으로 회귀분석을 해 볼 수 있는데, 오늘은 sklearn 패키지를 사용해보겠습니다.
먼저, sklearn에서 제공하는 linear_model을 import 하죠.
from sklearn.linear_model import LinearRegression lr = LinearRegression()
위와 같이 lr 변수를 생성했다면, 이제 우리는 lr 하나로 간단하게 회귀분석을 할 수 있습니다.
먼저, Y, X의 데이터를 정해야겟죠.
아까 위에서 정의한 데이터프레임 df에서 Y는 index가 될 것이고, X는 bmi로 정할 수 있습니다.
여기서 주의해야할 점이, X와 Y 모양 자체를 2d array를 바꿔줘야 합니다.
X = X.reshape(-1,1) Y = Y.reshape(-1,1)
이는 위와 같은 방법으로 쉽게 변환이 가능하며, 아래와 같은 모양으로 바뀌게 됩니다.
자, 모든 준비가 끝났습니다. 이제 회귀분석을 돌리면 됩니다.
lr.fit(X, Y)
X를 먼저 넣고 Y를 차례대로 변수로 입력해주고 실행하면 끝.
이제 회귀분석 결과를 보면, 아래와 같이 회귀 계수를 구할 수 있고, 여기서는 B1=949.435, B0=152.133으로 결과 값이 나왔네요.
앞선 시간에 배운 scatter plot에 회귀식을 그려보죠.
import matplotlib.pyplot as plt plt.scatter(X, Y) plt.plot(X, Y2, color=’red’) plt.title(‘y = {}*x + {}’.format(lr.coef_[0], lr.intercept_)) plt.show()
두 변수의 관계를 회귀식으로 표현하면 Target = 949 * BMI + 152이고,
이는 Target의 수치가 1 증가할 때마다 BMI가 949만큼 증가한다고 볼 수 있습니다.
2. 회귀모형의 검정 및 적합도 파악
이 회귀식이 통계적으로 유의한지, 변수가 유의하게 영향을 미치는 지, 그리고 얼만큼의 설명력을 가지는지 등의 여부를 확인해야 합니다.
A. F-statistic
도출된 회귀식이 회귀분석 모델 전체에 대해 통계적으로 의미가 있는지 파악
B. P-Value
각 변수가 종속변수에 미치는 영향이 유의한지 파악
C. 수정된 R제곱
회귀직선에 의하여 설명되는 변동이 총변동 중에서 차지하고 있는 상대적인 비율이 얼마인지 나타냄
즉, 회귀직선이 종속변수의 몇%를 설명할 수 있는지 확인
이번에는 다른 패키지를 통해 위에 나온 3가지 모두 확인해보겠습니다.
마법의 statsmodels 패키지를 아래와 같이 import 하고 회귀분석을 돌려보죠.
import statsmodels.api as sm results = sm.OLS(Y, sm.add_constant(X)).fit()
그리고 회귀분석의 결과를 results로 받은 후, 아래와 같이 summary()를 입력해주면 자세한 회귀분석 결과가 도출 됩니다.
결과를 보면 잔차에 대한 정보, 회귀계수에 대한 정보, R제곱, 검정통계량 F0 값과 P-value 값 등 자세하게 출력된 것을 확인할 수 있습니다.
A. F-statistic의 p-value 값은 Prob(F-statistic)으로 표현되는데, 이는 3.47e-42로 0.05보다 작기에 이 회귀식은 회귀분석 모델 전체에 대해 통계적으로 의미가 있다고 볼 수 있습니다.
B. 중간쯤에 보면 coef와 변수 x1의 p-value 값이 나와있습니다. 여기서 x1은 bmi이고 이 변수의 p-value가 0.000으로 표기 되어 있기에 0.05보다 작으므로 target을 설명하는데 유의하다고 판단할 수 있습니다.
C. 제일 위 부분에 R-squared와 Adj. R-squared가 표기되어 있는데, 값이 0.34정도로 이는 34%만큼의 설명력을 가진다고 판단할 수 있습니다. 참고로, 0에 가까울 수록 예측값을 믿을 수 없고 1에 가까울 수록 믿을 수 있다고 보면 됩니다.
이번에는 똑같은 원리로 중선형회귀분석을 해보죠.
<중선형회귀분석>
위 단순선형회귀분석과 비교했을 때 종속변수를 설명하는 독립변수가 두개 이상으로 증가했다고 생각하시면 됩니다.
기존에는 bmi만 독립변수로 가지고 있었다면, age와 sex를 추가해보죠.
그리고 위와 똑같은 순서로 회귀식을 돌려 결과 값을 보고 해석해 봅시다.
import statsmodels.api as sm results = sm.OLS(Y, sm.add_constant(X)).fit() results.summary()
회귀식은 Target = 926*bmi + 138*age – 36*sex + 152 로 도출이 될 수 있습니다.
A. F-statistic의 p-value 값은 Prob(F-statistic)으로 표현되는데, 이는 7.77e-41로 0.05보다 작기에 이 회귀식은 회귀분석 모델 전체에 대해 통계적으로 의미가 있다고 볼 수 있습니다.
B. 중간쯤에 보면 coef와 여러 변수들의 p-value 값이 나와있습니다. 여기서 x1과 x2는 변수의 p-value가 0.05 미만으로 유의미 하다고 볼 수 있지만 x3의 p-value는 0.569로 0.05보다 크기에 유의미하다고 판단할 수 없습니다. 즉, sex는 target을 설명하는데 유의하다고 판단할 수 없습니다.
C. 제일 위 부분에 R-squared와 Adj. R-squared가 표기되어 있는데, 값이 0.35정도로 이는 35%만큼의 설명력을 가진다고 판단할 수 있습니다.
앞선 결과와 비교 했을 때, 사실상 설명력이 더 높아지진 않았네요.
끝~
회귀분석 실시하기
판다스를 불러들인다.
실습을 위해 cars.csv를 다운로드 받아 연다.
statsmodels 를 불러들인다.
ols 함수로 회귀분석을 실시한다. 종속변수 ~ 독립변수 의 형태로 모형식을 쓴다. (수학에서는 $y = f(x)$처럼 종속변수를 왼쪽에, 독립변수를 오른쪽에 쓰는 것이 관습)
결과는 .summary() 메소드로 확인할 수 있다.
OLS Regression Results Dep. Variable: dist R-squared: 0.651 Model: OLS Adj. R-squared: 0.644 Method: Least Squares F-statistic: 89.57 Date: Thu, 23 Jan 2020 Prob (F-statistic): 1.49e-12 Time: 13:58:33 Log-Likelihood: -206.58 No. Observations: 50 AIC: 417.2 Df Residuals: 48 BIC: 421.0 Df Model: 1 Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975] Intercept -17.5791 6.758 -2.601 0.012 -31.168 -3.990 speed 3.9324 0.416 9.464 0.000 3.097 4.768
Omnibus: 8.975 Durbin-Watson: 1.676 Prob(Omnibus): 0.011 Jarque-Bera (JB): 8.189 Skew: 0.885 Prob(JB): 0.0167 Kurtosis: 3.893 Cond. No. 50.7
Warnings:[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[Python] 머신러닝 – 회귀분석(단순회귀분석, 다항회귀분석, 다중회귀분석)
Python [Python] 머신러닝 – 회귀분석(단순회귀분석, 다항회귀분석, 다중회귀분석) gp ・ URL 복사 본문 기타 기능 공유하기 신고하기 머신러닝 1. 종류 – 지도학습 : 정답을 알고 학습( 예측 : 회귀분석, 분류 : KNN) – 비지도학습 : 정답이 없는 상태에서 서로 비슷한 데이터끼리 그룹화 ( 군집 : k-means ) – 강화학습 : 예) 알파고 2. 머신러닝 프로젝트 데이터 정리 -> 데이터 분리(훈련데이터/검증데이터) -> 알고리즘 준비 -> 모형학습(훈련데이터) -> 예측(검증데이터) -> 모형평가 -> 모형활용 회귀분석(regression) : 연속적인 값 예측. 가격, 매출, 주가 등등의 연속성이 있는 데이터의 예측에 사용되는 알고리즘 – 설명(독립)변수 (예측에 사용되는 변수) -> 독립 변수 학습(머신러닝알고리즘 : 회귀분석) -> 예측(종속)변수 – 단순회귀분석 : 독립변수 X, 종속변수 Y (독립변수와 종속변수가 1:1) => Y = aX + b # 기본 라이브러리 불러오기 import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns # 데이터 가져오기 df = pd.read_csv(“auto-mpg.csv”, header=None) # 열 이름 지정 df.columns=[‘mpg’,’cylinders’,’displacement’,’horsepower’,’weight’, ‘acceleration’,’model year’,’origin’,’name’] df.head() mpg cylinders displacement … model year origin name 0 18.0 8 307.0 … 70 1 chevrolet chevelle malibu 1 15.0 8 350.0 … 70 1 buick skylark 320 2 18.0 8 318.0 … 70 1 plymouth satellite 3 16.0 8 304.0 … 70 1 amc rebel sst 4 17.0 8 302.0 … 70 1 ford torino [5 rows x 9 columns] df.info()
RangeIndex: 398 entries, 0 to 397 Data columns (total 9 columns): # Column Non-Null Count Dtype — —— ————– —– 0 mpg 398 non-null float64 1 cylinders 398 non-null int64 2 displacement 398 non-null float64 3 horsepower 398 non-null object 4 weight 398 non-null float64 5 acceleration 398 non-null float64 6 model year 398 non-null int64 7 origin 398 non-null int64 8 name 398 non-null object dtypes: float64(4), int64(3), object(2) memory usage: 28.1+ KB df.describe() mpg cylinders … model year origin count 398.000000 398.000000 … 398.000000 398.000000 mean 23.514573 5.454774 … 76.010050 1.572864 std 7.815984 1.701004 … 3.697627 0.802055 min 9.000000 3.000000 … 70.000000 1.000000 25% 17.500000 4.000000 … 73.000000 1.000000 50% 23.000000 4.000000 … 76.000000 1.000000 75% 29.000000 8.000000 … 79.000000 2.000000 max 46.600000 8.000000 … 82.000000 3.000000 [8 rows x 7 columns] df.horsepower.unique() array([‘130.0’, ‘165.0’, ‘150.0’, ‘140.0’, ‘198.0’, ‘220.0’, ‘215.0’, ‘225.0’, ‘190.0’, ‘170.0’, ‘160.0’, ‘95.00’, ‘97.00’, ‘85.00’, ‘88.00’, ‘46.00’, ‘87.00’, ‘90.00’, ‘113.0’, ‘200.0’, ‘210.0’, ‘193.0’, ‘?’, ‘100.0’, ‘105.0’, ‘175.0’, ‘153.0’, ‘180.0’, ‘110.0’, ‘72.00’, ‘86.00’, ‘70.00’, ‘76.00’, ‘65.00’, ‘69.00’, ‘60.00’, ‘80.00’, ‘54.00’, ‘208.0’, ‘155.0’, ‘112.0’, ‘92.00’, ‘145.0’, ‘137.0’, ‘158.0’, ‘167.0’, ‘94.00’, ‘107.0’, ‘230.0’, ‘49.00’, ‘75.00’, ‘91.00’, ‘122.0’, ‘67.00’, ‘83.00’, ‘78.00’, ‘52.00’, ‘61.00’, ‘93.00’, ‘148.0’, ‘129.0’, ‘96.00’, ‘71.00’, ‘98.00’, ‘115.0’, ‘53.00’, ‘81.00’, ‘79.00’, ‘120.0’, ‘152.0’, ‘102.0’, ‘108.0’, ‘68.00’, ‘58.00’, ‘149.0’, ‘89.00’, ‘63.00’, ‘48.00’, ‘66.00’, ‘139.0’, ‘103.0’, ‘125.0’, ‘133.0’, ‘138.0’, ‘135.0’, ‘142.0’, ‘77.00’, ‘62.00’, ‘132.0’, ‘84.00’, ‘64.00’, ‘74.00’, ‘116.0’, ‘82.00’], dtype=object) # 데이터 전처리 1.horsepower 컬럼의 ?값을 결측값(np.nan)으로 변경하기 df[‘horsepower’].replace(‘?’,np.nan, inplace=True) df[‘horsepower’].isnull().sum() # 6 print(df.info()) # 물음표 6개가 결측치로 바뀜 RangeIndex: 398 entries, 0 to 397 Data columns (total 9 columns): # Column Non-Null Count Dtype — —— ————– —– 0 mpg 398 non-null float64 1 cylinders 398 non-null int64 2 displacement 398 non-null float64 3 horsepower 392 non-null object 4 weight 398 non-null float64 5 acceleration 398 non-null float64 6 model year 398 non-null int64 7 origin 398 non-null int64 8 name 398 non-null object dtypes: float64(4), int64(3), object(2) memory usage: 28.1+ KB None 2. 누락 데이터의 행을 삭제하기. dropna() df.dropna(subset=[‘horsepower’],axis=0,inplace=True) print(df.info()) # horsepower가 object(?때문에) => 숫자형태로 바꿔주기. Int64Index: 392 entries, 0 to 397 Data columns (total 9 columns): # Column Non-Null Count Dtype — —— ————– —– 0 mpg 392 non-null float64 1 cylinders 392 non-null int64 2 displacement 392 non-null float64 3 horsepower 392 non-null object 4 weight 392 non-null float64 5 acceleration 392 non-null float64 6 model year 392 non-null int64 7 origin 392 non-null int64 8 name 392 non-null object dtypes: float64(4), int64(3), object(2) memory usage: 30.6+ KB None 3. horsepower 데이터의 형을 실수형으로 변환 pd.set_option(‘display.max_columns’,10) # 10까지 컬럼을 조회하기 설정 df.describe() # horsepower컬럼이 숫자가 아니기 때문에 조회 안 됨. mpg cylinders displacement weight acceleration \ count 392.000000 392.000000 392.000000 392.000000 392.000000 mean 23.445918 5.471939 194.411990 2977.584184 15.541327 std 7.805007 1.705783 104.644004 849.402560 2.758864 min 9.000000 3.000000 68.000000 1613.000000 8.000000 25% 17.000000 4.000000 105.000000 2225.250000 13.775000 50% 22.750000 4.000000 151.000000 2803.500000 15.500000 75% 29.000000 8.000000 275.750000 3614.750000 17.025000 max 46.600000 8.000000 455.000000 5140.000000 24.800000 model year origin count 392.000000 392.000000 mean 75.979592 1.576531 std 3.683737 0.805518 min 70.000000 1.000000 25% 73.000000 1.000000 50% 76.000000 1.000000 75% 79.000000 2.000000 max 82.000000 3.000000 df[‘horsepower’]=df[‘horsepower’].astype(float) 4. 분석에 활용할 속성(열)을 선택. 연비(mpg), 실린더(cylinders), 출력(horsepower), 중량(weight) ndf = df[[‘mpg’,’cylinders’,’horsepower’,’weight’]] ndf.head() mpg cylinders horsepower weight 0 18.0 8 130.0 3504.0 1 15.0 8 165.0 3693.0 2 18.0 8 150.0 3436.0 3 16.0 8 150.0 3433.0 4 17.0 8 140.0 3449.0 # matplot으로 mpg, weight 변수의 산점도 작성하기 ndf.plot(kind=’scatter’, x =’weight’, y=’mpg’, c=’coral’, s=10, figsize=(10,5)) plt.show() # seaborn으로 산점도 그리기 fig = plt.figure(figsize=(10,5)) ax1 = fig.add_subplot(1,2,1) ax2 = fig.add_subplot(1,2,2) sns.regplot(x =’weight’, y=’mpg’,data = ndf, ax= ax1) sns.regplot(x =’weight’, y=’mpg’,data = ndf, ax= ax2, fit_reg=False) plt.show() # jointplot 그리기 sns.jointplot(x=’weight’, y =’mpg’, data=ndf) sns.jointplot(x=’weight’, y =’mpg’, kind=’reg’,data=ndf) plt.show() Previous image Next image # seaborn pairplot sns.pairplot(ndf, kind=’reg’) plt.show() 회귀분석 산점도 결과를 보면, 직선보다는 곡선의 형태가 더 예측하기 좋다. (단순 선형 회귀 분석은 직선으로 분석하는 방법) -> 이 데이터에서는 높은 정확도를 위해 곡선형태의 회귀선이 좋다. 1. 단순회귀분석 : 두 변수간의 관계를 직선형태로 분석하는 알고리즘. Y = aX + b 2. 다항회귀분석 : 두 변수간의 관계를 곡선형태로 분석하는 알고리즘. Y = aX**2 + bX + c 3. 다중회귀분석 : 여러개의 독립변수가 종속변수에 영향을 주고, 선형관계를 갖는 경우. Y= b + a1*X1 + a2*X2 + … + an*Xn 1. 단순회귀분석 # 독립변수 : X (독립변수는 여러개가 들어갈 수 있으므로 데이터 프레임 형태 가능) X = ndf[[‘weight’]] print(type(X)) # # 종속변수 : y y = ndf[‘mpg’] print(type(y)) # 시리즈형태 # 데이터셋 구분 – 훈련용(train data) / 검증용(test data) # 훈련데이터, 검증데이터 분리 (7:3으로 분리) # random_state=10 : 추출에 사용되는 상수. 랜덤의 seed 값과 비슷. 분리되는 데이터의 유지성을 위한 설정 from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X,Y,test_size=0.3, random_state=10) print(‘train data 개수: ‘, len(X_train)) print(‘test data 개수: ‘, len(X_test)) train data 개수: 274 test data 개수: 118 X_train[:10] weight 38 4209.0 172 2223.0 277 3410.0 196 2164.0 357 2615.0 342 2385.0 276 2795.0 280 3245.0 125 3102.0 82 2506.0 # sklearn 라이브러리에서 선형회귀분석 모듈 가져오기 from sklearn.linear_model import LinearRegression # 단순회귀분석 모형 객체 생성 lr = LinearRegression() # train data를 가지고 모형 학습 # X_train : 훈련데이터. y_train : 정답 lr.fit(X_train, y_train) # 결정계수(R 제곱) r_square = lr.score(X_test, y_test) print(r_square) # 0.6822458558299325 # 기울기 print(“기울기 a”, lr.coef_) # 기울기 a [-0.00775343] # y 절편 print(“y 절편 b”, lr.intercept_) # y 절편 b 46.710366257280086 # 테스트하기. 전체 데이터 사용. # y_hat 은 y랑 똑같으면 됨. y_hat : 예측한 값 y_hat = lr.predict(X) # 평가 # 원래 값 y와 예측된 값 y_hat 데이터를 그래프로 작성하기 plt.figure(figsize=(10,5)) ax1 = sns.kdeplot(y, label=”y”) # 실제 mpg 데이터의 그래프(정답). kdeplot : 빈도수, 밀도에 해당 ax2 = sns.kdeplot(y_hat, label=’y_hat’, ax=ax1) # 예측한 값 plt.legend() plt.show() 2. 다항회귀분석 # 다항식 변환 from sklearn.preprocessing import PolynomialFeatures poly = PolynomialFeatures(degree=2) # 2차항 적용 X_train_poly=poly.fit_transform(X_train) # X_train 데이터를 2차항 형식에 맞도록 적용 print(‘원 데이터: ‘, X_train.shape) # 원 데이터: (274, 1) print(‘2차항 변환 데이터: ‘, X_train_poly.shape) # 2차항 변환 데이터: (274, 3) # 다항회귀분석 pr = LinearRegression() # 선형회귀분석 객체 pr.fit(X_train_poly, y_train) # 학습하기 X_test_poly = poly.fit_transform(X_test) # X_test : 검증 데이터 . 2차항 형태로 변경 r_square = pr.score(X_test_poly, y_test) # 결정계수(R-제곱) r_square # 0.7087009262975685 y_hat_test = pr.predict(X_test_poly) # 2차항 형태로 변경된 테스트데이터 # 산점도 그리기 fig = plt.figure(figsize=(10,5)) ax = fig.add_subplot(1,1,1) # 원 데이터의 산점도 출력하기 ax.plot(X_train, y_train, ‘o’, label = ‘Train Data’) # 모형. 검증데이터(X_test)와 다항 회귀분석의 결과값(y_hat_test) ax.plot(X_test, y_hat_test, ‘r+’, label = ‘Predicted Value’) ax.legend(loc=’best’) plt.xlabel(‘weight’) plt.ylabel(‘mpg’) plt.show() # 모형 전체 그래프 작성하기 X_poly = poly.fit_transform(X) y_hat = pr.predict(X_poly) plt.figure(figsize=(10,5)) ax1 = sns.kdeplot(y, label=’y’) ax2 = sns.kdeplot(y_hat,label=’y_hat’, ax=ax1) plt.legend() plt.show() 3. 다중회귀분석 # 독립변수와 종속변수 구분 from sklearn.linear_model import LinearRegression lr = LinearRegression() X = ndf[[‘cylinders’,’horsepower’,’weight’]] Y = ndf[‘mpg’] # train data와 test data로 구분 (7:3 비율) X_train, X_test, y_train, y_test = train_test_split(X,Y,test_size=0.3, random_state=10) print(‘훈련 데이터: ‘, X_train.shape) print(‘검증 데이터:’, X_test.shape) 훈련 데이터: (274, 3) 검증 데이터: (118, 3) # X_train 훈련시키기 lr.fit(X_train,y_train) # 결정계수(R제곱) 조회하기 r_square = lr.score(X_test, y_test) r_square # 0.6939048496695597 # 기울기 print(“회귀식의 기울기 (a)”, lr.coef_) 회귀식의 기울기 (a) [-0.60691288 -0.03714088 -0.00522268] # y 절편 print(“회귀식의 y절편 (b)”, lr.intercept_) 회귀식의 y절편 (b) 46.41435126963405 # test 데이터로 예측하기 y_hat = lr.predict(X_test) # 예측된 데이터와 실데이터를 kdeplot 으로 출력하기 plt.figure(figsize=(10,5)) ax1 = sns.kdeplot(y_test, label=”y_test”) ax2 = sns.kdeplot(y_hat, label=’y_hat’, ax=ax1) plt.legend() plt.show() # 원 데이터로 예측하기 y_hat = lr.predict(X) # 예측된 데이터와 실데이터를 kdeplot 으로 출력하기 plt.figure(figsize=(10,5)) ax1 = sns.kdeplot(Y, label=”Y”) ax2 = sns.kdeplot(y_hat, label=’y_hat’, ax=ax1) plt.legend() plt.show() # 회귀 분석의 간단한 예 # 공부시간 : 독립변수, 시험점수 : 종속변수 x = [[10,3],[5,2],[9,3],[7,3],[8,2]] # [공부시간,학년] y = [[100],[50],[90],[77],[85]] # 시험점수, 리스트 형태도 가능 # 학습시키기 from sklearn.linear_model import LinearRegression model = LinearRegression() # 선형회귀분석 객체 생성하기 # 선형회귀분석 객체를 이용하여 학습시키기 model.fit(x,y) # 예측하기 result = model.predict([[7,2]]) # 7시간 공부, 2학년 print(“예상점수:”, result) 예상점수: [[72.27272727]] 210715 문제 1. seoul_5.csv 데이터를 이용하여 2021년 7월 15일의 평균기온을 예측해보기. # 단순 회귀 분석 import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns plt.rc(‘font’, family =’Malgun Gothic’) seoul = pd.read_csv(“seoul_5.csv”, encoding=”cp949″) seoul.info() RangeIndex: 40221 entries, 0 to 40220 Data columns (total 5 columns): # Column Non-Null Count Dtype — —— ————– —– 0 날짜 40221 non-null object 1 지점 40221 non-null int64 2 평균기온(℃) 39465 non-null float64 3 최저기온(℃) 39464 non-null float64 4 최고기온(℃) 39463 non-null float64 dtypes: float64(3), int64(1), object(1) memory usage: 1.5+ MB seoul.head() 날짜 지점 평균기온(℃) 최저기온(℃) 최고기온(℃) 0 1907-10-01 108 13.5 7.9 20.7 1 1907-10-02 108 16.2 7.9 22.0 2 1907-10-03 108 16.2 13.1 21.3 3 1907-10-04 108 16.5 11.2 22.0 4 1907-10-05 108 17.6 10.9 25.4 seoul[‘년도’] = seoul[‘날짜’].apply(lambda x: x[:4]) seoul0715 = seoul[seoul[‘날짜’].apply(lambda x: x[5:])==’07-15′] seoul0715.head() 날짜 지점 평균기온(℃) 최저기온(℃) 최고기온(℃) 년도 288 1908-07-15 108 23.0 20.6 26.5 1908 653 1909-07-15 108 26.6 23.7 30.4 1909 1018 1910-07-15 108 23.2 20.0 27.8 1910 1383 1911-07-15 108 22.8 20.1 25.3 1911 1749 1912-07-15 108 20.8 18.2 23.3 1912 seoul0715.info() Int64Index: 110 entries, 288 to 40034 Data columns (total 6 columns): # Column Non-Null Count Dtype — —— ————– —– 0 날짜 110 non-null object 1 지점 110 non-null int64 2 평균기온(℃) 108 non-null float64 3 최저기온(℃) 108 non-null float64 4 최고기온(℃) 108 non-null float64 5 년도 110 non-null object dtypes: float64(3), int64(1), object(2) memory usage: 6.0+ KB seoul0715.dropna(subset=[“평균기온(℃)”],axis=0, inplace=True) # 결측값 가진 행 제거 from sklearn.linear_model import LinearRegression model = LinearRegression() X = seoul0715[[“년도”]] Y = seoul0715[‘평균기온(℃)’] model.fit(X, Y) result = model.predict([[‘2021’]]) print(result) # [24.88918934] # 다항 회귀 분석 from sklearn.linear_model import LinearRegression model = LinearRegression() from sklearn.preprocessing import PolynomialFeatures # 다항식 변환 poly = PolynomialFeatures(degree=2) # 2차항 적용 X = seoul0715[[“년도”]] Y = seoul0715[‘평균기온(℃)’] X_poly=poly.fit_transform(X) model.fit(X_poly, Y) X_test_poly = poly.fit_transform([[‘2021’]]) result = model.predict(X_test_poly) print(result) # [25.0177538] # 다중 회귀 분석 import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns plt.rc(‘font’, family =’Malgun Gothic’) seoul = pd.read_csv(“data/seoul_5.csv”, encoding=”cp949″) seoul.info() seoul.head() seoul[‘년도’] = seoul[‘날짜’].apply(lambda x: x[:4]) seoul0715 = seoul[seoul[‘날짜’].apply(lambda x: x[5:])==’07-15′] seoul0715.head() seoul0715.info() seoul0715.dropna(subset=[“평균기온(℃)”,”최저기온(℃)”,”최고기온(℃)”],axis=0, inplace=True) from sklearn.linear_model import LinearRegression model = LinearRegression() X = seoul0715[[“년도”,”최저기온(℃)”,”최고기온(℃)”]] Y = seoul0715[‘평균기온(℃)’] model.fit(X, Y) result = model.predict([[‘2021’,24,33]]) print(result) # [27.82109479] 2. 7월15일에 해당하는 평균온도를 산점도,회귀선 출력하기 seoul0715.info() seoul0715[‘년도’] =seoul0715[‘년도’].astype(“int64”) seoul0715.info() Int64Index: 108 entries, 288 to 40034 Data columns (total 6 columns): # Column Non-Null Count Dtype — —— ————– —– 0 날짜 108 non-null object 1 지점 108 non-null int64 2 평균기온(℃) 108 non-null float64 3 최저기온(℃) 108 non-null float64 4 최고기온(℃) 108 non-null float64 5 년도 108 non-null int64 dtypes: float64(3), int64(2), object(1) memory usage: 5.9+ KB fp1 = np.polyfit(seoul0715[‘년도’], seoul0715[‘평균기온(℃)’], 2) f1 = np.poly1d(fp1) fx = np.linspace(1907, 2017, 108) seoul0715.plot(kind=’scatter’, x=’년도’, y=’평균기온(℃)’, c=’coral’, s=10, figsize=(10, 5)) plt.plot(fx, f1(fx), ls=’dashed’, lw=3, color=’g’) plt.show() fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(1, 1, 1) sns.regplot(x=’년도’, y=’평균기온(℃)’, data=seoul0715, ax=ax1) plt.show() sns.jointplot(x=’년도’, y=’평균기온(℃)’, data=seoul0715, kind=’reg’) plt.show() # seaborn pariplot sns.pairplot(seoul0715,kind=’reg’) plt.show() from sklearn.linear_model import LinearRegression lr = LinearRegression() X = ndf[[‘cylinders’,’horsep 인쇄
So you have finished reading the 파이썬 회귀 분석 topic article, if you find this article useful, please share it. Thank you very much. See more: 파이썬 sklearn 회귀분석, 파이썬 다중회귀분석, 파이썬 회귀분석 예제, 파이썬 회귀분석 코드, 파이썬 선형회귀분석, 파이썬 회귀분석 그래프, 파이썬 단순회귀분석, 파이썬 회귀분석 시각화
